
| A. | 22 | B. | 18 | C. | 26 | D. | -24 |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
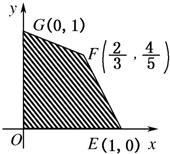 如图,目标函数z=kx-y的可行域为四边形OEFG(含边界),若点F($\frac{2}{3}$,$\frac{4}{5}$)是目标函数的最优解,则k的取值范围是( )
如图,目标函数z=kx-y的可行域为四边形OEFG(含边界),若点F($\frac{2}{3}$,$\frac{4}{5}$)是目标函数的最优解,则k的取值范围是( )| A. | (-$\frac{12}{5}$,$\frac{4}{5}$) | B. | ($\frac{3}{10},\frac{12}{5}$) | C. | [-$\frac{12}{5}$,-$\frac{3}{10}$] | D. | [-$\frac{3}{10}$,-$\frac{12}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-2,1) | B. | (-1,2,1) | C. | (1,-2,-1) | D. | (1,2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 年生活垃圾无害化处理量y | 0.7 | 1.1 | 1.4 | 2.2 | 2.6 | 3.0 | 3.7 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:解答题
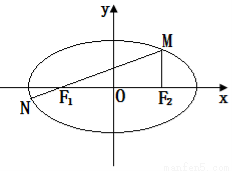
设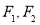 分别是椭圆
分别是椭圆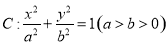 的左右焦点,
的左右焦点,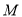 是
是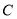 上一点,且
上一点,且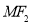 与
与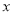 轴垂直,直线
轴垂直,直线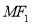 与
与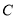 的另一个交点为
的另一个交点为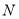 .
.
(1)若直线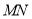 的斜率为
的斜率为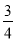 ,求
,求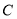 的离心率;
的离心率;
(2)若直线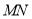 在
在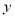 轴上的截距为2,且
轴上的截距为2,且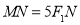 ,求椭圆
,求椭圆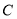 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com