
【题目】将一块圆心角为120°,半径为20cm的扇形钢片裁出一块矩形钢片,如图有两种裁法:使矩形一边在扇形的一条半径OA上,或者让矩形一边与弦AB平行,试问哪种裁法能使截得的矩形钢片面积最大?并求出这个最大值.

【答案】见解析
【解析】试题分析:对甲种裁法分析设![]() ,则矩形的一边为
,则矩形的一边为![]() ,一边为
,一边为![]() ,则得出面积,利用正弦函数取最值的方法求出最大面积;对乙种裁法分析设
,则得出面积,利用正弦函数取最值的方法求出最大面积;对乙种裁法分析设![]() 利用三角函数表示出
利用三角函数表示出![]() 长和
长和![]() ,进而表示出面积,利用余弦函数取最大值的方法求出最大面积,比较看哪个面积大即可.
,进而表示出面积,利用余弦函数取最大值的方法求出最大面积,比较看哪个面积大即可.
试题解析:如图甲,要使矩形面积最大,则O为其一顶点且另一顶点M在弧AB上,设∠MOA=θ,则矩形PMNO的面积S1=20·sinθ·20cosθ=200sin2θ,
当θ=45°时,S1有最大值,为200cm2;
如图乙,设∠MOA=θ,在△OMQ中,由正弦定理得QM=![]() .
.
由图形的对称性知,∠AOB的平分线OC为其对称轴,于是MN=2OM·sin(60°-θ),
∴矩形PQMN的面积S2=QM·MN=![]()
2sinθsin(60°-θ)= ![]() [cos(2θ-600)-cos60°].
[cos(2θ-600)-cos60°].
当θ=30°时,S2有最大值为![]() cm2,又∵
cm2,又∵![]() >200;
>200;
故用第二种方法可截得的矩形钢片面积最大,最大面积为![]() cm2.
cm2.


科目:高中数学 来源: 题型:
【题目】吉安一中举行了一次“环保知识竞赛”活动,为了解本了次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() 分)作为样本(样本容量为
分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照 ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() 的数据).
的数据).
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从竞赛学生成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的
名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的![]() 名同学中得分在
名同学中得分在![]() 的学生人数恰有一人的概率.
的学生人数恰有一人的概率.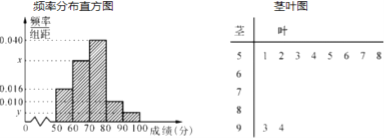
查看答案和解析>>
科目:高中数学 来源: 题型:
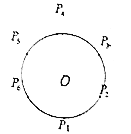
【题目】如图,设![]() 为单位圆上逆时针均匀分布的六个点,现从这六个点中任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量
为单位圆上逆时针均匀分布的六个点,现从这六个点中任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量![]() .
.
(1)求![]() 的概率;
的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年5月,我省南昌市遭受连日大暴雨天气,某网站就“民众是否支持加大修建城市地下排水设施的资金投入”进行投票,按照南昌暴雨前后两个时间收集有效投票,暴雨后的投票收集了![]() 份,暴雨前的投票也收集了
份,暴雨前的投票也收集了![]() 份,所得统计结果如下表:
份,所得统计结果如下表:

已知工作人与从所有投票中任取一个,取到“不支持投入”的投票的概率为![]() .
.
(1)求列表中数据的值;
(2)能够有多大的把握认为南昌暴雨对民众是否赞成加大对修建城市地下排水设施的投入有关系?
附: 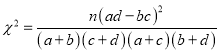
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明和爸爸周末到湿地公园进行锻炼,两人上午9:00从公园入口出发,沿相同路线匀速运动,小明15分钟后到达目的地,此时爸爸离出发地的路程为1200米,小明到达目的地后立即按原路匀速返回,与爸爸相遇后,和爸爸一起从原路返回出发地.小明、爸爸在锻炼过程中离出发地的路程与小明出发的时间的函数关系如图.
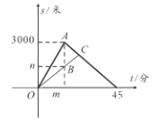
(1)图中![]() ________,
________, ![]() _______;
_______;
(2)求小明和爸爸相遇的时刻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据悉遵义市红花岗区、汇川区2017年现有人口总数为110万人,如果年自然增长率为![]() %,试解答以下问题:
%,试解答以下问题:
(1)写出经过![]() 年后,遵义市人口总数
年后,遵义市人口总数![]() (单位:万人)关于
(单位:万人)关于![]() 的函数关系式;
的函数关系式;
(2)计算10年以后遵义市人口总数(精确到0.1万人);
(3)计算经过多少年后遵义市人口将达到150万人(精确到1年)
(参考数据: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com