
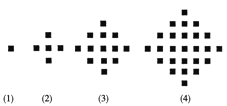
【题目】某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1) 求出![]() ,
,![]() ,
,![]() 并猜测
并猜测![]() 的表达式;
的表达式;
(2) 求证:![]() +
+![]() +
+![]() +…+
+…+![]()
![]() .
.
【答案】(1) f(2)=5,f(3)=13,f(4)=25,f(5)=25+4×4=41.f(n)=2n2-2n+1.
(2)略
【解析】
本试题主要是考查了数列的归纳猜想思想的运用,根据前几项。来猜想并运用数学归纳法加以证明。
(1)结合题目中的 递推关系式可知前几项的值,并猜想结论。
(2)分为两步骤进行,先证明n取第一个值时成立,再假设n=k时成立,证明n=k+1时也成立即可。
解: (1)∵f(1)=1,f(2)=5,f(3)=13,f(4)=25,∴f(5)=25+4×4=41.
∵f(2)-f(1)=4=4×1,f(3)-f(2)=8=4×2,f(4)-f(3)=12=4×3,f(5)-f(4)=16=4×4,
由上式规律得出f(n+1)-f(n)=4n. ∴f(n)-f(n-1)=4(n-1),f(n-1)-f(n-2)=4·(n-2),
f(n-2)-f(n-3)=4·(n-3),…
f(2)-f(1)=4×1,
∴f(n)-f(1)=4[(n-1)+(n-2)+…+2+1]=2(n-1)·n,∴f(n)=2n2-2n+1(n≥2),
又n=1时,f(1)也适合f(n).
∴f(n)=2n2-2n+1. --------6分

![]() ---------------12分
---------------12分


科目:高中数学 来源: 题型:
【题目】设集合A,B是R中两个子集,对于![]() ,定义:
,定义: 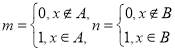 .①若
.①若![]() ;则对任意
;则对任意![]() ;②若对任意
;②若对任意![]() ,则
,则![]() ;③若对任意
;③若对任意![]() ,则A,B的关系为
,则A,B的关系为![]() .上述命题正确的序号是______. (请填写所有正确命题的序号)
.上述命题正确的序号是______. (请填写所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,把圆
,把圆![]() 上每一点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线
上每一点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线![]() ,且倾斜角为
,且倾斜角为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)当![]() 时,求曲线
时,求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的参数方程;
的参数方程;
(2)求点![]() 到
到![]() 两点的距离之积的最小值.
两点的距离之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的![]() ,全世界近
,全世界近![]() 人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨):一位居民的月用水量不超过
(吨):一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由;
(3)若该市政府希望使![]() 的居民每月的用水不按议价收费,估计
的居民每月的用水不按议价收费,估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工企业2018年年底投入100万元,购入一套污水处理设备。该设备每年的运转费用是0.5万元,此外,每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元。设该企业使用该设备![]() 年的年平均污水处理费用为
年的年平均污水处理费用为![]() (单位:万元)
(单位:万元)
(1)用![]() 表示
表示![]() ;
;
(2)当该企业的年平均污水处理费用最低时,企业需重新更换新的污水处理设备。则该企业几年后需要重新更换新的污水处理设备。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若a=0时,求函数![]() 的零点;
的零点;
(2)若a=4时,求函数![]() 在区间[2,5]上的最大值和最小值;
在区间[2,5]上的最大值和最小值;
(3)当![]() 时,不等式
时,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数y=2sin![]() 的图象的一条对称轴是x=
的图象的一条对称轴是x=![]() ;
;
②函数y=tanx的图象关于点![]() 对称;
对称;
③若sin![]() =sin
=sin![]() ,则x1-x2=kπ,其中k∈Z;
,则x1-x2=kπ,其中k∈Z;
④函数![]() ,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围为(1,3).
,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围为(1,3).
其中正确的有____(填写所有正确命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com