
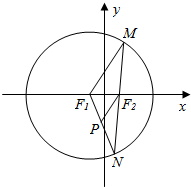
 已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.
已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.分析 (1)由平行线成比例,结合椭圆的定义,可得P的轨迹方程;
(2)讨论直线斜率不存在和存在,设出直线方程,代入椭圆方程,运用韦达定理,化简整理,即可得到定值.
解答 解:(1)∵F2P∥MF1,
∴$\frac{P{F}_{2}}{M{F}_{1}}$=$\frac{PN}{{F}_{1}N}$,可得$\frac{P{F}_{2}}{4}$=$\frac{4-P{F}_{1}}{4}$,即有PF1+PF2=4>F1F2=2,
∴点P的轨迹是以F1,F2为焦点,长轴长2a的椭圆,
即有a=2,c=1,b=$\sqrt{3}$,其轨迹方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)(Ⅰ)若lAB的斜率存在时,设lAB为:y=k(x-1),
联立$\frac{x^2}{4}+\frac{y^2}{3}=1$,可得:(3+4k2)x2-8k2x+4k2-12=0,
不妨设A(x1,y1),B(x2,y2)(x2<1<x1),则$\left\{\begin{array}{l}{x_1}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}}\\{x_1}{x_2}=\frac{{4{k^2}-12}}{{3+4{k^2}}}\end{array}\right.$,
∴$\frac{1}{{|{F_2}A|}}+\frac{1}{{|{F_2}B|}}=\frac{1}{{\sqrt{1+{k^2}}|{{x_1}-1}|}}+\frac{1}{{\sqrt{1+{k^2}}|{{x_2}-1}|}}=\frac{1}{{\sqrt{1+{k^2}}}}({\frac{1}{{{x_1}-1}}+\frac{1}{{1-{x_2}}}})$
=$\frac{1}{{\sqrt{1+{k^2}}}}({\frac{{1-{x_2}+{x_1}-1}}{{({{x_1}-1})({1-{x_2}})}}})=\frac{1}{{\sqrt{1+{k^2}}}}({\frac{{{x_1}-{x_2}}}{{({{x_1}+{x_2}})-{x_1}•{x_2}-1}}})$
=$\frac{1}{{\sqrt{1+{k^2}}}}({\frac{{\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}•{x_2}}}}{{({{x_1}+{x_2}})-{x_1}•{x_2}-1}}})=\frac{1}{{\sqrt{1+{k^2}}}}({\frac{{\sqrt{{{({\frac{{8{k^2}}}{{3+4{k^2}}}})}^2}-4×\frac{{4{k^2}-12}}{{3+4{k^2}}}}}}{{\frac{{8{k^2}}}{{3+4{k^2}}}-\frac{{4{k^2}-12}}{{3+4{k^2}}}-1}}})$
=$\frac{1}{{\sqrt{1+{k^2}}}}({\frac{{\frac{{12\sqrt{1+{k^2}}}}{{3+4{k^2}}}}}{{\frac{9}{{3+4{k^2}}}}}})=\frac{12}{9}=\frac{4}{3}$;
(Ⅱ)若lAB的斜率不存在时,此时lAB:x=1,
则$A({1,\frac{3}{2}}),B({1,-\frac{3}{2}})$,
此时$\frac{1}{{|{F_2}A|}}+\frac{1}{{|{F_2}B|}}=\frac{2}{3}+\frac{2}{3}=\frac{4}{3}$.
综上可知,变化直线l,则$\frac{1}{{|{F_2}A|}}+\frac{1}{{|{F_2}B|}}$为定值$\frac{4}{3}$.
点评 本题考查轨迹的方程的求法,注意运用定义,考查直线和椭圆方程联立,运用韦达定理,考查运算能力,属于难题.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|a=kπ+$\frac{π}{2}$,k∈Z} | B. | {a|a=kπ,k∈Z} | ||
| C. | {a|a=2kπ+$\frac{π}{2}$,k∈Z} | D. | {a|a=kπ或a=kπ+$\frac{π}{2}$,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为A1B1中点,F为CC1中点,如图.
已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为A1B1中点,F为CC1中点,如图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com