
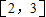 上有最大值4,最小值1,设函数
上有最大值4,最小值1,设函数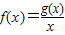 .
.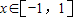 时恒成立,求实数k的取值范围.
时恒成立,求实数k的取值范围.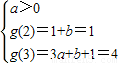 ,或
,或 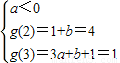 ,解得a、b的值,即可得到函数f(x)的解析式.
,解得a、b的值,即可得到函数f(x)的解析式.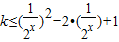 ,在
,在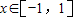 时,设
时,设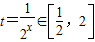 ,则k≤(t-1)2,
,则k≤(t-1)2,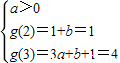 ,解得
,解得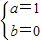 .
.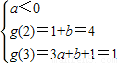 ,解得
,解得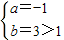 .(舍去)
.(舍去) 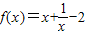 . …(7分)
. …(7分)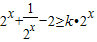 ,∴
,∴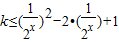 .…(10分)
.…(10分)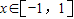 时,设
时,设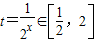 ,∴k≤(t-1)2,
,∴k≤(t-1)2, ≤t≤2,且t≠1.
≤t≤2,且t≠1.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
|
| g(x) |
| x |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| g(x) |
| x |
| 4 |
| |2x-1| |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省常州市奔牛高级中学高三(上)第一次段考数学试卷(解析版) 题型:解答题
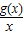 .
.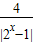 -3)=0有三个相异的实数根,求实数t的取值范围.
-3)=0有三个相异的实数根,求实数t的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏州市张家港市梁丰高级中学高三(上)周日数学试卷(5)(解析版) 题型:解答题
 .
. -3)=0有三个相异的实数根,求实数t的取值范围.
-3)=0有三个相异的实数根,求实数t的取值范围.查看答案和解析>>
科目:高中数学 来源:2012年上海市虹口区高考数学二模试卷(文科)(解析版) 题型:解答题
 上有最大值4,最小值1,设函数
上有最大值4,最小值1,设函数 .
. 时恒成立,求实数k的取值范围.
时恒成立,求实数k的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com