【答案】
分析:(1)根据平面向量数量积的运算,化简f(x)=2cos(2x-

)+2,再根据三角函数性质求解.
(2)设

=(m,n),先求出函数f(x) 的图象平移后对应的函数g(x),根据中心对称性求出m,n的值或表达式.再结合条件要求确定长度最小的

.
解答:解:(1)∵f(x)=(
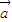
+

)
2+

sin 2x=3cos
2x+sin
2x+

sin2x=2cos(2x-

)+2 …(3分)
∴f(x)≥0,当且仅当2x-

=2kπ+π,即x=kπ+
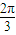
,k∈Z时取到等号.
∴函数f(x)的最小值是0,此时x的集合是{x|x=kπ+
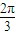
,k∈Z} …(6分)
(2)设

=(m,n),函数f(x) 的图象平移后对应的函数为g(x),则g(x)=2cos[2(x-m)-
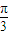
]+2+n
由题意函数g(x)的图象关于坐标原点中心对称,得
cos[2(0-m)-
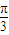
]=0,且2+n=0,解得m=

kπ+
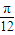
,k∈Z,且n=-2 …(8分)
①当m=kπ+

,k∈Z时,g(x)=2cos(2x-

)=2sin 2x,在[0,
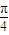
]上单调递增,不符合题意,舍去;
②当m=kπ+

,k∈Z时,g(x)=2cos(2x+

)=-2sin 2x,在[0,

]上单调递减,符合题意.…(10分)
∴

=( kπ+

,-2),k∈Z【若求出的结果是(kπ+
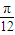
,-2),给(10分)】
∴长度最小的

=(-

,-2)…(12分)
点评:本题考查平面向量数量积的运算,三角函数性质,考查分析解决问题、分类讨论、计算能力.

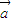 =(
=(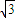 cos x,0),
cos x,0),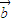 =(0,sin x),记函数f(x)=(
=(0,sin x),记函数f(x)=(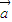 +
+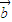 )2+
)2+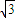 sin 2x,
sin 2x,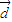 平移后,得到的图象关于坐标原点中心对称且在[0,
平移后,得到的图象关于坐标原点中心对称且在[0, ]上单调递减,求长度最小的
]上单调递减,求长度最小的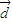 .
. )+2,再根据三角函数性质求解.
)+2,再根据三角函数性质求解. =(m,n),先求出函数f(x) 的图象平移后对应的函数g(x),根据中心对称性求出m,n的值或表达式.再结合条件要求确定长度最小的
=(m,n),先求出函数f(x) 的图象平移后对应的函数g(x),根据中心对称性求出m,n的值或表达式.再结合条件要求确定长度最小的 .
.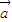 +
+ )2+
)2+ sin 2x=3cos2x+sin2x+
sin 2x=3cos2x+sin2x+ sin2x=2cos(2x-
sin2x=2cos(2x- )+2 …(3分)
)+2 …(3分) =2kπ+π,即x=kπ+
=2kπ+π,即x=kπ+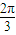 ,k∈Z时取到等号.
,k∈Z时取到等号.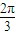 ,k∈Z} …(6分)
,k∈Z} …(6分) =(m,n),函数f(x) 的图象平移后对应的函数为g(x),则g(x)=2cos[2(x-m)-
=(m,n),函数f(x) 的图象平移后对应的函数为g(x),则g(x)=2cos[2(x-m)-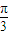 ]+2+n
]+2+n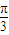 ]=0,且2+n=0,解得m=
]=0,且2+n=0,解得m= kπ+
kπ+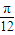 ,k∈Z,且n=-2 …(8分)
,k∈Z,且n=-2 …(8分) ,k∈Z时,g(x)=2cos(2x-
,k∈Z时,g(x)=2cos(2x- )=2sin 2x,在[0,
)=2sin 2x,在[0,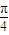 ]上单调递增,不符合题意,舍去;
]上单调递增,不符合题意,舍去; ,k∈Z时,g(x)=2cos(2x+
,k∈Z时,g(x)=2cos(2x+ )=-2sin 2x,在[0,
)=-2sin 2x,在[0, ]上单调递减,符合题意.…(10分)
]上单调递减,符合题意.…(10分) =( kπ+
=( kπ+ ,-2),k∈Z【若求出的结果是(kπ+
,-2),k∈Z【若求出的结果是(kπ+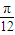 ,-2),给(10分)】
,-2),给(10分)】 =(-
=(- ,-2)…(12分)
,-2)…(12分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案