
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求实数
,求实数![]() 的值.
的值.
(2)若![]() ,
,![]() ,求正实数
,求正实数![]() 的取值范围.
的取值范围.
【答案】(1)0(2)![]()
【解析】
(1)求得![]() 和
和![]() ,由
,由![]() ,
,![]() ,得
,得![]() ,令
,令![]() ,令导数求得函数
,令导数求得函数![]() 的单调性,利用
的单调性,利用![]() ,即可求解.
,即可求解.
(2)解法一:令![]() ,利用导数求得
,利用导数求得![]() 的单调性,转化为
的单调性,转化为![]() ,令
,令![]() (
(![]() ),利用导数得到
),利用导数得到![]() 的单调性,分类讨论,即可求解.
的单调性,分类讨论,即可求解.
解法二:可利用导数,先证明不等式,![]() ,
,![]() ,
,![]() ,
,
令![]() (
(![]() ),利用导数,分类讨论得出函数的单调性与最值,即可求解.
),利用导数,分类讨论得出函数的单调性与最值,即可求解.
(1)由题意,得![]() ,
,![]() ,
,
由![]() ,
,![]() …①,得
…①,得![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
又![]() ,所以当
,所以当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
所以![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
故方程①有且仅有唯一解![]() ,实数
,实数![]() 的值为0.
的值为0.
(2)解法一:令![]() (
(![]() ),
),
则![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
故![]()
![]()
![]() .
.
令![]() (
(![]() ),
),
则![]() .
.
(i)若![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
所以![]() ,满足题意.
,满足题意.
(ii)若![]() 时,
时,![]() ,满足题意.
,满足题意.
(iii)若![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减,
单调递减,
所以![]() .不满足题意.
.不满足题意.
综上述:![]() .
.
解法二:先证明不等式,![]() ,
,![]() ,
,![]() …(*).
…(*).
令![]() ,
,
则当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以![]() ,即
,即![]() .
.
变形得,![]() ,所以
,所以![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() .
.
又由上式得,当![]() 时,
时,![]() ,
,![]() ,
,![]() .
.
因此不等式(*)均成立.
令![]() (
(![]() ),
),
则![]() ,
,
(i)若![]() 时,当
时,当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
故![]()
![]()
![]() .
.
(ii)若![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
所以![]()
![]() .
.
因此,①当![]() 时,此时
时,此时![]() ,
,![]() ,
,![]() ,
,
则需![]()
由(*)知,![]() ,(当且仅当
,(当且仅当![]() 时等号成立),所以
时等号成立),所以![]() .
.
②当![]() 时,此时
时,此时![]() ,
,![]() ,
,
则当![]() 时,
时,![]()
![]()
![]() (由(*)知);
(由(*)知);
当![]() 时,
时,![]() (由(*)知).故对于任意
(由(*)知).故对于任意![]() ,
,![]() .
.
综上述:![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() 为椭圆短轴端点,若
为椭圆短轴端点,若![]() 为直角三角形且周长为
为直角三角形且周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() ,
,![]() 斜率的乘积为
斜率的乘积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中央广播电视总台2019主持人大赛》是中央人民广播电视总台成立后推出的第一个电视大赛,由撒贝宁担任主持人,康辉、董卿担任点评嘉宾,敬一丹、鲁健、朱迅、俞虹、李洪岩等17位担任专业评审.从2019年10月26日起,每周六20:00在中央电视台综合频道播出.某传媒大学为了解大学生对主持人大赛的关注情况,分别在大一和大二两个年级各随机抽取了100名大学生进行调查.下图是根据调查结果绘制的学生场均关注比赛的时间频率分布直方图和频数分布表,并将场均关注比赛的时间不低于80分钟的学生称为“赛迷”.
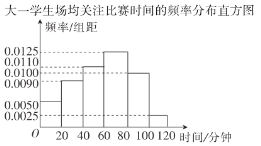
大二学生场均关注比赛时间的频数分布表
时间分组 | 频数 |
| 12 |
| 20 |
| 24 |
| 22 |
| 16 |
| 6 |
(1)将频率视为概率,估计哪个年级的大学生是“赛迷”的概率大,请说明理由;
(2)已知抽到的100名大一学生中有男生50名,其中10名为“赛迷”试完成下面的![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为“赛迷”与性别有关.
的把握认为“赛迷”与性别有关.
非“赛迷” | “赛迷” | 合计 | |
男 | |||
女 | |||
合计 |
附: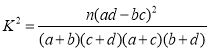 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过其右焦点
,过其右焦点![]() 与长轴垂直的直线与椭圆在第一象限交于点
与长轴垂直的直线与椭圆在第一象限交于点![]() ,且
,且![]() .
.
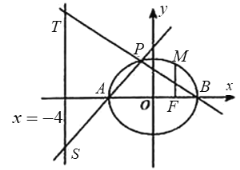
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,点
,点![]() 是椭圆上的动点,且点
是椭圆上的动点,且点![]() 与点
与点![]() ,
,![]() 不重合,直线
不重合,直线![]() ,
,![]() 与直线
与直线![]() 分别交于点
分别交于点![]() ,
,![]() ,求证:以线段
,求证:以线段![]() 为直径的圆过定点
为直径的圆过定点![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过其右焦点
,过其右焦点![]() 与长轴垂直的直线与椭圆在第一象限交于点
与长轴垂直的直线与椭圆在第一象限交于点![]() ,且
,且![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,点
,点![]() 是椭圆上的动点,且点
是椭圆上的动点,且点![]() 与点
与点![]() ,
,![]() 不重合,直线
不重合,直线![]() ,
,![]() 与直线
与直线![]() 分别交于点
分别交于点![]() ,
,![]() ,求证:以线段
,求证:以线段![]() 为直径的圆过定点.
为直径的圆过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取60名学生,将期中考试的物理成绩(均为整数)分成六段:![]() ,
,![]() ,
,![]() ,…,
,…,![]() 后得到如图频率分布直方图.
后得到如图频率分布直方图.
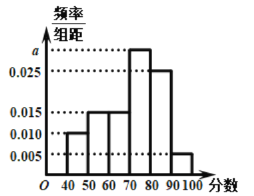
(1)根据频率分布直方图,估计众数和中位数;
(2)用分层抽样的方法从![]() 的学生中抽取一个容量为5的样本,从这五人中任选两人参加补考,求这两人的分数至少一人落在
的学生中抽取一个容量为5的样本,从这五人中任选两人参加补考,求这两人的分数至少一人落在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设D是圆O:x2+y2=16上的任意一点,m是过点D且与x轴垂直的直线,E是直线m与x轴的交点,点Q在直线m上,且满足2|EQ|![]() |ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
|ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程.
(2)已知点P(2,3),过F(2,0)的直线l交曲线C于A,B两点,交直线x=8于点M.判定直线PA,PM,PB的斜率是否依次构成等差数列?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com