
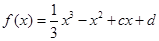
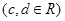 ,其图象为曲线
,其图象为曲线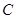 ,点
,点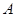 为曲线
为曲线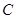 上的动点,在点
上的动点,在点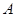 处作曲线
处作曲线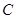 的切线
的切线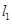 与曲线
与曲线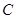 交于另一点
交于另一点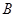 ,在点
,在点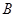 处作曲线
处作曲线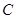 的切线
的切线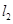 .
.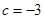 时,求函数
时,求函数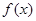 的单调区间;
的单调区间;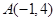 时,
时,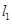 的方程为
的方程为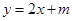 ,求实数
,求实数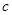 和
和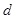 的值;
的值;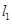 、
、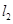 的斜率分别为
的斜率分别为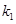 、
、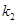 ,试问:是否存在常数
,试问:是否存在常数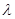 ,使得
,使得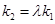 ?若存在,求出
?若存在,求出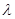 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.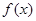 的单调递增区间是
的单调递增区间是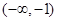 和
和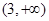 ;单调递减区间是
;单调递减区间是 ;(2)
;(2)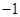 ,
,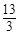 ;(3)
;(3)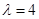 .
.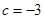 代入到函数
代入到函数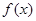 中,求导,解出
中,求导,解出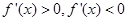 的
的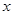 的取值范围,从而能够写出函数的单增区间和单减区间;(2)将切点
的取值范围,从而能够写出函数的单增区间和单减区间;(2)将切点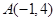 代入到函数表达式中,求出
代入到函数表达式中,求出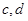 的关系,再将
的关系,再将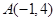 代入到
代入到 中,求出最终
中,求出最终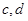 的值;(3)设
的值;(3)设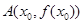 ,写出函数在
,写出函数在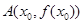 处的切线,并与曲线联立,得到关于
处的切线,并与曲线联立,得到关于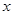 的方程
的方程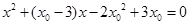 ,再设
,再设 ,根据韦达定理表示出
,根据韦达定理表示出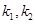 ,再利用
,再利用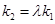 ,得出
,得出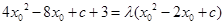 ,化简成
,化简成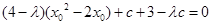 ,则能够得到
,则能够得到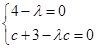 ,进而能够求出
,进而能够求出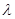 的值.
的值.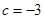 时,
时,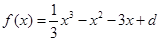
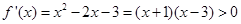 ,解得
,解得 或
或 ;
;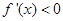 ,解得
,解得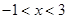
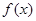 的单调递增区间是
的单调递增区间是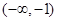 和
和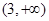 ;单调递减区间是
;单调递减区间是 .
.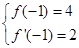 ,即
,即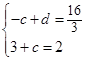 ,
,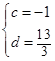
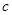 和
和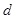 的值分别是
的值分别是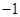 和
和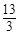 .
. 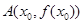 ,则
,则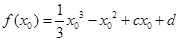 ,
,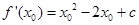

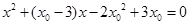
 ,则由韦达定理得
,则由韦达定理得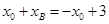 ,∴
,∴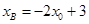
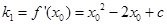 ;
;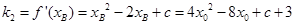
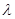 使得
使得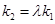 ,则
,则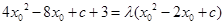 ,
,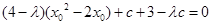 ,∴
,∴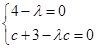 ,解得
,解得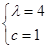
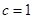 时,存在常数
时,存在常数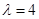 使得
使得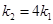 ;
; 时,不存在
时,不存在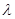 ,使得
,使得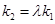 .
. 

科目:高中数学 来源:不详 题型:解答题
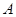 、
、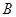 ,根据市场调查与预测,A项目的利润与投资成正比,其关系如图甲,B项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)
,根据市场调查与预测,A项目的利润与投资成正比,其关系如图甲,B项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)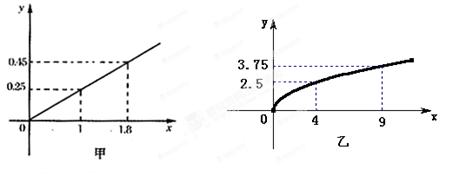
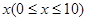 万元投资A项目, 10-x万元投资B项目.h(x)表示投资A项目所得利润与投资B项目所得利润之和.求h(x)的最大值,并指出x为何值时,h(x)取得最大值.
万元投资A项目, 10-x万元投资B项目.h(x)表示投资A项目所得利润与投资B项目所得利润之和.求h(x)的最大值,并指出x为何值时,h(x)取得最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
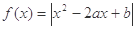
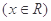 ,给出下列命题:
,给出下列命题: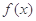 必是偶函数;
必是偶函数;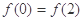 时,
时,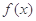 的图象关于直线
的图象关于直线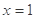 对称;
对称;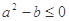 ,则
,则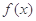 在区间
在区间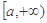 上是增函数;
上是增函数;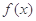 有最大值
有最大值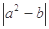 .
. | A.(3) | B.(2)(3) | C.(3)(4) | D.(1)(2)(3) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
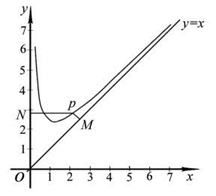
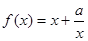 定义域为
定义域为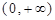 ,且
,且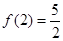 .设点
.设点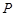 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点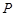 分别作直线
分别作直线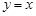 和
和 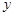 轴的垂线,垂足分别为
轴的垂线,垂足分别为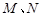 .
.
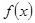 的单调递减区间(不必证明);
的单调递减区间(不必证明);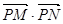 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;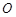 为坐标原点,求四边形
为坐标原点,求四边形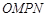 面积的最小值.
面积的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
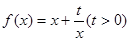 和点
和点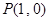 ,过点
,过点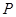 作曲线
作曲线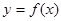 的两条切线
的两条切线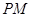 、
、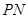 ,切点分别为
,切点分别为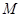 、
、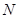 .
.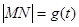 ,试求函数
,试求函数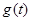 的表达式;
的表达式;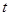 ,使得
,使得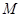 、
、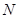 与
与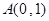 三点共线.若存在,求出
三点共线.若存在,求出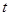 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.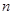 ,在区间
,在区间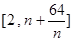 内总存在
内总存在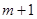 个实数
个实数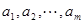 ,
,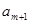 ,使得不等式
,使得不等式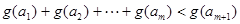 成立,求
成立,求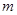 的最大值.
的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com