
【题目】如果你留心使会发现,汽车前灯后的反射镜呈抛物线的形状,把抛物线沿它的对称轴旋转一周,就会形成一个抛物面.这种抛物面形状,正是我们熟悉的汽车前灯的反射镜形状,这种形状使车灯既能够发出明亮的、照射很远的平行光束,又能发出较暗的,照射近距离的光线.我们都知道常规的前照灯主要是由灯泡、反射镜和透镜三部分组成,明亮的光束,是由位于抛物面形状反射镜焦点的光源射出的,灯泡位于抛物面的焦点上,灯泡发出的光经抛物面反射镜反射形成平行光束,再经过配光镜的散射、偏转作用,以达到照亮路面的效果,这样的灯光我们通常称为远光灯:而较暗的光线,不是由反射镜焦点的光源射出的,光线的行进与抛物线的对称轴不平行,光线只能向上和向下照射,所以照射距离并不远,如果把向上射出的光线遮住.车灯就只能发出向下的、射的很近的光线了.请用数学的语言归纳表达远光灯的照明原理,并证明.
【答案】远光灯照明原理:由抛物线的焦点所在的光源发出的光线经抛物线反射后与抛物线的对称轴平行,证明见解析
【解析】
设![]() 为抛物线上一点,法线与
为抛物线上一点,法线与![]() 轴交于
轴交于![]() ,反射光线为
,反射光线为![]() ,
,![]() 为抛物线的焦点,
为抛物线的焦点,![]() 的斜率,根据角的正切值,证明
的斜率,根据角的正切值,证明![]() 即可.
即可.
远光灯照明原理:由抛物线的焦点所在的光源发出的光线经抛物线反射后与抛物线的对称轴平行.
证明:不妨设抛物线方程为:y2=2px(p>0),焦点为F,P为抛物线上一点,FP的反射光线为PN,
如图所示:设抛物线过点P的切线为直线l,法线交x轴于M,
由光的反射性质可知∠FPM=∠MPN,
由y2=2px,不妨设P在第一象限,P(![]() ,y0),
,y0),
当y0=0时,直线l与y轴重合,显然PN与x轴重合,
当y0≠0时,设直线l的斜率为k,
则直线l的方程为:y=k(x![]() )+y0,
)+y0,
代入抛物线方程可得:ky2﹣2py﹣ky02+2py0=0,
令△=4p2﹣4k(2py0﹣ky02)=0可得k![]() ,
,
故法线PM的斜率为![]() .
.
不妨设P在第一象限,设∠PMx=α,∠PFM=β,∠NPM=θ,
则tanα![]() ,tanβ
,tanβ ,
,
∴tanθ=tan∠FPM=tan(α﹣β) .
.
∴tanθ+tanα=0,故α+θ=π,
∴PN∥x轴.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四边形ABED中,AB//DE,AB![]() BE,点C在AB上,且AB
BE,点C在AB上,且AB![]() CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE
CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE![]() .
.
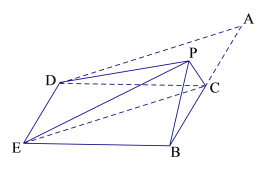
(1)求证:平面PBC ![]() 平面DEBC;
平面DEBC;
(2)求三棱锥P-EBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人造地球卫星绕地球运行遵循开普勒行星运动定律:如图,卫星在以地球的中心为焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积守恒规律,即卫星的向径(卫星与地心的连线)在相同的时间内扫过的面积相等设该椭圆的长轴长、焦距分别为![]() ,
,![]() .某同学根据所学知识,得到下列结论:
.某同学根据所学知识,得到下列结论:

①卫星向径的取值范围是![]()
②卫星向径的最小值与最大值的比值越大,椭圆轨道越扁
③卫星在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间
④卫星运行速度在近地点时最小,在远地点时最大
其中正确的结论是( )
A.①②B.①③C.②④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】卵形线是常见曲线的一种,分笛卡尔卵形线和卡西尼卵形线,卡西尼卵形线是平面内与两个定点(叫焦点)的距离之积等于常数的点的轨迹.某同学类比椭圆与双曲线对卡西尼卵形线进行了相关性质的探究,设F1(﹣c,0),F2(c,0)是平面内的两个定点,|PF1||PF2|=a2(a是常数).得出卡西尼卵形线的相关结论:①该曲线既是轴对称图形也是中心对称图形;②若a=c,则曲线过原点;③若0<a<c,其轨迹为线段.其中正确命题的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,若函数
时,若函数![]() 的导函数
的导函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,其横坐标分别为
两点,其横坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,且
,且![]() ,
, ![]() 恰为函数
恰为函数![]() 的零点,求证:
的零点,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式![]() 表示的平面区别为
表示的平面区别为![]() .区域
.区域![]() 内的动点
内的动点![]() 到直线
到直线![]() 和直线
和直线![]() 的距离之积为2.记点
的距离之积为2.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .过点
.过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 垂直于
垂直于![]() 轴,
轴,![]() 为曲线
为曲线![]() 上一点,求
上一点,求![]() 的取值范围;
的取值范围;
(3)若以线段![]() 为直径的圆与
为直径的圆与![]() 轴相切,求直线
轴相切,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,前
为等差数列,前![]() 项和为
项和为![]() ,
,![]() 是首项为
是首项为![]() 的等比数列,且公比大于
的等比数列,且公比大于![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,
,![]() 为数列
为数列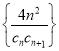 的前
的前![]() 项和,求不超过
项和,求不超过![]() 的最大整数.
的最大整数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱![]() 的侧棱与底面垂直,
的侧棱与底面垂直,![]() ,
,![]() ,M是
,M是![]() 的中点,
的中点,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上,且满足
上,且满足![]() .
.
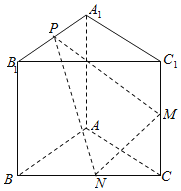
(1)证明:![]() .
.
(2)当![]() 取何值时,直线
取何值时,直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 最大?并求该角最大值的正切值.
最大?并求该角最大值的正切值.
(3)若平面![]() 与平面
与平面![]() 所成的二面角为
所成的二面角为![]() ,试确定P点的位置.
,试确定P点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() 与抛物线
与抛物线![]() 的焦点重合,原点到过点
的焦点重合,原点到过点![]() ,
,![]() 的直线的距离是
的直线的距离是![]() .
.
![]() 1
1![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 2
2![]() 设动直线
设动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,过
,过![]() 作
作![]() 的垂线与直线
的垂线与直线![]() 交于点
交于点![]() ,求证:点
,求证:点![]() 在定直线上,并求出定直线的方程.
在定直线上,并求出定直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com