
【题目】一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱喷出的水柱的高度,某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°,沿点A向北偏东30°前进100 m到达点B,在B点测得水柱顶端的仰角为30°,则水柱的高度是( )
A. 50 mB. 100 m
C. 120 mD. 150 m
【答案】A
【解析】
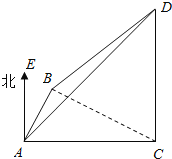
如图所示,设水柱CD的高度为h.在Rt△ACD中,由∠DAC=45°,可得AC=h.由∠BAE=30°,可得∠CAB=60°.在Rt△BCD中,∠CBD=30°,可得BC=![]() .在△ABC中,由余弦定理可得:BC2=AC2+AB2﹣2ACABcos60°.代入即可得出.
.在△ABC中,由余弦定理可得:BC2=AC2+AB2﹣2ACABcos60°.代入即可得出.
如图所示,
设水柱CD的高度为h.
在Rt△ACD中,∵∠DAC=45°,∴AC=h.
∵∠BAE=30°,∴∠CAB=60°.
又∵B,A,C在同一水平面上,∴△BCD是以C为直角顶点的直角三角形,
在Rt△BCD中,∠CBD=30°,∴BC=![]() .
.
在△ABC中,由余弦定理可得:BC2=AC2+AB2﹣2ACABcos60°.
∴(![]() )2=h2+1002﹣
)2=h2+1002﹣![]() ,
,
化为h2+50h﹣5000=0,解得h=50.
故选:A.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】从某校高中男生中随机选取100名学生,将他们的体重(单位: ![]() )数据绘制成频率分布直方图,如图所示.
)数据绘制成频率分布直方图,如图所示.
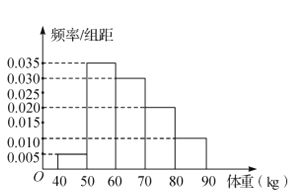
(1)估计该校的100名同学的平均体重(同一组数据以该组区间的中点值作代表);
(2)若要从体重在![]() ,
, ![]() 内的两组男生中,用分层抽样的方法选取5人,再从这5人中随机抽取3人,记体重在
内的两组男生中,用分层抽样的方法选取5人,再从这5人中随机抽取3人,记体重在![]() 内的人数为
内的人数为![]() ,求其分布列和数学期望
,求其分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司要了解某商品的年广告费![]() (单位:万元)对年销售额
(单位:万元)对年销售额![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年销售额
和年销售额![]() 数据作了初步调研,得到下面的表格:
数据作了初步调研,得到下面的表格:
年广告费 | 2 | 3 | 4 | 5 |
年销售额 | 26 | 39 | 49 | 54 |
用广告费作解释变量,年销售额作预报变量,且![]() 适宜作为年销售额
适宜作为年销售额![]() 关于年广告费
关于年广告费![]() 的回归方程类型.
的回归方程类型.
(1)根据表中数据,建立![]() 关于
关于![]() 的回归方程.
的回归方程.
(2)已知商品的年利润![]() 与
与![]() ,
,![]() 的关系式为
的关系式为![]() ,根据(1)中的结果,估计年广告费
,根据(1)中的结果,估计年广告费![]() 为何值时(小数点后保留两位),年利润的预报值最大?
为何值时(小数点后保留两位),年利润的预报值最大?
(对于数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为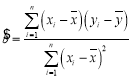 ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
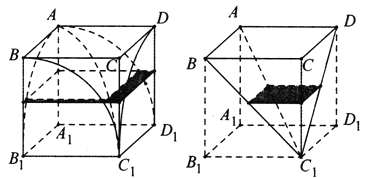
【题目】为推导球的体积公式,刘徽制造了一个牟合方盖(在一个正方体内作两个互相垂直的内切圆柱,这两个圆柱的公共部分叫做牟合方盖),但没有得到牟合方盖的体积.200年后,祖暅给出牟合方盖的体积计算方法,其核心过程被后人称为祖暅原理:缘幂势既同,则积不容异.意思是,夹在两个平行平面间的两个几何体被平行于这两个平行平面的任意平面所截,如果截面的面积总相等,那么这两个几何体的体积也相等.现在截取牟合方盖的八分之一,它的外切正方体![]() 的棱长为1,如图所示,根据以上信息,则该牟合方盖的体积为( )
的棱长为1,如图所示,根据以上信息,则该牟合方盖的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,点
,点![]() .
.
(1)求抛物线![]() 的顶点坐标;
的顶点坐标;
(2)若抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,连接
,连接![]() ,并延长交抛物线
,并延长交抛物线![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)将抛物线![]() 作适当的平移,得抛物线
作适当的平移,得抛物线![]() ,若
,若![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 得最大值.
得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l、m,平面α、β,下列命题正确的是 ( )
A. l∥β,lαα∥β
B. l∥β,m∥β,lα,mαα∥β
C. l∥m,lα,mβα∥β
D. l∥β,m∥β,lα,mα,l∩m=Mα∥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为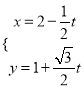 (
(![]() 为参数).
为参数).
(I)写出直线![]() 的一般方程与曲线
的一般方程与曲线![]() 的直角坐标方程,并判断它们的位置关系;
的直角坐标方程,并判断它们的位置关系;
(II)将曲线![]() 向左平移
向左平移![]() 个单位长度,向上平移
个单位长度,向上平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]() ,设曲线
,设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,设曲线
,设曲线![]() 上任一点为
上任一点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下给出了4个命题:
(1)两个长度相等的向量一定相等;
(2)相等的向量起点必相同;
(3)若![]() ,且
,且![]() ,则
,则![]() ;
;
(4)若向量![]() 的模小于
的模小于![]() 的模,则
的模,则![]() .
.
其中正确命题的个数共有( )
A.3 个B.2 个C.1 个D.0个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子商务公司随机抽取1000名网购者进行调查.这1000名购物者2018年网购金额(单位:万元)均在区间![]() 内,样本分组为:
内,样本分组为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,购物金额的频率分布直方图如下:
,购物金额的频率分布直方图如下:
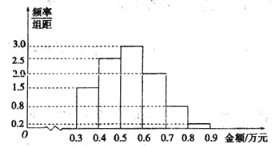
电子商务公司决定给购物者发放优惠券,其金额(单位:元)与购物金额关系如下:
购物金额分组 |
|
|
|
|
发放金额 | 50 | 100 | 150 | 200 |
(1)求这1000名购物者获得优惠券金额的平均数;
(2)以这1000名购物者购物金额落在相应区间的频率作为概率,求一个购物者获得优惠券金额不少于150元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com