已知函数
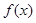
定义域为R,且
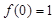
,对任意
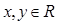
恒有
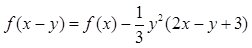
,
(1)求函数
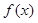
的表达式;
(2)若方程
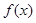
=
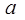
有三个实数解,求实数
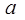
的取值范围;
(1)
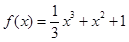
(2)
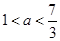
第一问中,利用因为
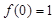
,对任意
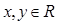
恒有
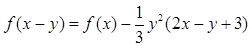
,
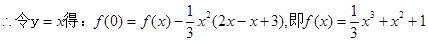
第二问中,因为方程
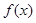
=

有三个实数解,所以
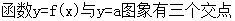
又因为
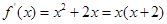
当

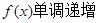
;
当
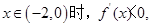
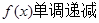
从而得到范围。
解:(1)因为
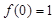
,对任意
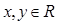
恒有
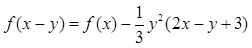
,
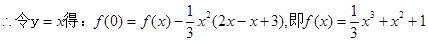
(2)因为方程
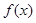
=

有三个实数解,所以
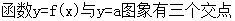
又因为
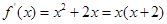
,当

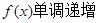
;
当
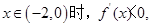
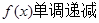
;当
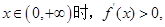
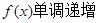
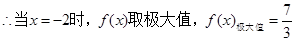
,

练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:填空题
已知函数
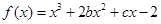
的图象在与
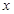
轴交点处的切线方程是
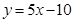
.则函数
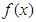
的解析式为
__________。
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
曲线
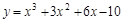
的切线中,斜率最小的的切线方程为
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分12分)
已知函数
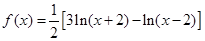
,
(1)求
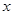
为何值时,
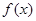
在
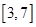
上取得最大值;
(2)设
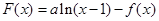
,若
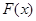
是单调递增函数,求
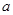
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设函数
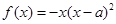
(Ⅰ)当
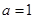
时,求曲线
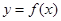
在点
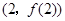
处的切线方程;
(Ⅱ)
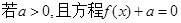
有三个不同的实数解,求
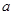
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数
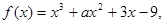
已知
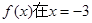
时取得极值,则a=( )
查看答案和解析>>

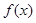 定义域为R,且
定义域为R,且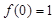 ,对任意
,对任意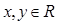 恒有
恒有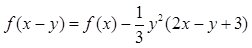 ,
,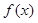 的表达式;
的表达式;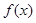 =
=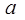 有三个实数解,求实数
有三个实数解,求实数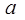 的取值范围;
的取值范围; 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案