练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设各项都是正数的等比数列{}，Sn为前n项和，且S10=10，S30=70，那么S40=______

    【答案】150

    【解析】

    根据数列{}是等比数列，Sn为前n项和，且S10＝10≠0可得，S10，S20﹣S10，S30﹣S20，S40﹣S30也成等比数列，即可得到结果．

    根据数列{}是等比数列，Sn为前n项和，且S10＝10≠0可得数列S10，S20﹣S10，S30﹣S20，S40﹣S30成等比数列，

    因此有（S20﹣S10）2＝S10（S30﹣S20），即（S20﹣10）2＝10（70﹣S20），

    故S20＝﹣20或S20＝30，又 ，S20＞0，因此S20＝30，S20﹣S10＝20，S30﹣S20＝40，

    故S40﹣S30＝80，S40＝150．

    故答案为：150．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列的首项为1，且，数列满足，，对任意，都有.

    （1）求数列、的通项公式；

    （2）令，数列的前项和为.若对任意的，不等式恒成立，试求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（2﹣a）（x﹣1）﹣2lnx，（a∈R）． （Ⅰ）当a=1时，求f（x）的单调区间；
    （Ⅱ）若函数f（x）在（0， ）上无零点，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数列中，已知，且对于任意正整数n都有．

    （1）令，求数列的通项公式；

    （2）求的通项公式；

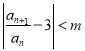    （3）设是一个正数，无论为何值，都有一个正整数使成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）一个盒子里装有三张卡片，分别标记有数字，，，这三张卡片除标记的数字外完全相同。随机有放回地抽取次，每次抽取张，将抽取的卡片上的数字依次记为，，.

    （Ⅰ）求“抽取的卡片上的数字满足”的概率；

    （Ⅱ）求“抽取的卡片上的数字，，不完全相同”的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若数列{}的前n项和Sn=2-2．

    （1）求数列{}的通项公式；

    （2）若bn=log，Sn=b1+b2+…+bn，对任意正整数n，Sn+（n+m）＜0恒成立，试求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校对高二年段的男生进行体检，现将高二男生的体重（kg）数据进行整理后分成6组，并绘制部分频率分布直方图（如图所示）．已知第三组[60，65）的人数为200．根据一般标准，高二男生体重超过65kg属于偏胖，低于55kg属于偏瘦．观察图形的信息，回答下列问题：

    （1）求体重在[60，65）内的频率，并补全频率分布直方图；

    （2）用分层抽样的方法从偏胖的学生中抽取6人对日常生活习惯及体育锻炼进行调查，则各组应分别抽取多少人？

    （3）根据频率分布直方图，估计高二男生的体重的中位数与平均数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校高三年级共有学生名，为了解学生某次月考的情况，抽取了部分学生的成绩（得分均为整数，满分为分）进行统计，绘制出如下尚未完成的频率分布表：

    分组

    频数

    频率

    （1）补充完整题中的频率分布表；

    （2）若成绩在为优秀，估计该校高三年级学生在这次月考中，成绩优秀的学生约为多少人.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面凸四边形中（凸四边形指没有角度数大于的四边形），.

    （1）若，，求；

    （2）已知，记四边形的面积为.

    ① 求的最大值；

    ② 若对于常数，不等式恒成立，求实数的取值范围.（直接写结果，不需要过程）

    查看答案和解析>>

    同步练习册答案