
【题目】已知函数![]() ,下列结论中错误的是( )
,下列结论中错误的是( )
A.![]() 的图像关于点
的图像关于点![]() 对称B.
对称B.![]() 的图像关于直线
的图像关于直线![]() 对称
对称
C.![]() 的最大值为
的最大值为![]() D.
D.![]() 是周期函数
是周期函数
【答案】C
【解析】
根据对称性,周期性最值的概念结合三角函数的运算,逐项判断即可.
对于A,因为f(π﹣x)+f(x)=sin(π﹣x)sin(2π﹣2x)+sinxsin2x=0,所以A正确;
对于B,f(2π﹣x)=sin(2π﹣x)sin(4π﹣2x)=sinxsin2x=f(x),所以![]() 的图像关于直线
的图像关于直线![]() 对称,所以B正确;
对称,所以B正确;
对于C,f(x)=sinxsin2x=2sin2xcosx=2(1﹣cos2x)cosx=2cosx﹣2cos3x,令t=cosx,则t∈[﹣1,1],f(x)=g(t)=2t﹣2t3,令g′(t)=2﹣6t2=0,得,t![]() ,
,
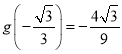 ,
, ,
,![]() ,
,![]() ,所以
,所以![]() 的最大值是
的最大值是![]() ,从而
,从而![]() 的最大值是
的最大值是![]() ,故C错误;
,故C错误;
对于D,因为![]() ,即f(2π+x)=f(x),故2π为函数f(x)的一个周期,故D正确;
,即f(2π+x)=f(x),故2π为函数f(x)的一个周期,故D正确;
故选:C.


科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形,一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.分形几何学不仅让人们感悟到科学与艺木的融合,数学与艺术审美的统一,而且还有其深刻的科学方法论意义.如图,由波兰数学家谢尔宾斯基1915年提出的谢尔宾斯基三角形就属于-种分形,具体作法是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形.

若在图④中随机选取-点,则此点取自阴影部分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大数据时代对于现代人的数据分析能力要求越来越高,数据拟合是一种把现有数据通过数学方法来代入某条数式的表示方式,比如![]() ,
,![]()
![]() ,2,
,2,![]() ,n是平面直角坐标系上的一系列点,用函数
,n是平面直角坐标系上的一系列点,用函数![]() 来拟合该组数据,尽可能使得函数图象与点列
来拟合该组数据,尽可能使得函数图象与点列![]() 比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数
比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数![]() 的拟合误差为:
的拟合误差为:![]() .已知平面直角坐标系上5个点的坐标数据如表:
.已知平面直角坐标系上5个点的坐标数据如表:
x | 1 | 3 | 5 | 7 | 9 |
y | 12 |
| 4 |
| 12 |
![]() 若用一次函数
若用一次函数![]() 来拟合上述表格中的数据,求该函数的拟合误差
来拟合上述表格中的数据,求该函数的拟合误差![]() 的最小值,并求出此时的函数解析式
的最小值,并求出此时的函数解析式![]() ;
;
![]() 若用二次函数
若用二次函数![]() 来拟合题干表格中的数据,求
来拟合题干表格中的数据,求![]() ;
;
![]() 请比较第
请比较第![]() 问中的
问中的![]() 和第
和第![]() 问中的
问中的![]() ,用哪一个函数拟合题目中给出的数据更好?
,用哪一个函数拟合题目中给出的数据更好?![]() 请至少写出三条理由
请至少写出三条理由![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有穷数列![]() 共有
共有![]() 项
项![]() ,首项
,首项![]() ,设该数列的前
,设该数列的前![]() 项和为
项和为![]() ,且
,且![]()
![]() 其中常数
其中常数![]() .
.
(1)求证:数列![]() 是等比数列
是等比数列
(2)若![]() ,数列
,数列![]() 满足
满足![]()
![]() ,求出数列
,求出数列![]() 的通项公式
的通项公式
(3)若(2)中的数列![]() 满足不等式
满足不等式![]() ,求出
,求出![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为双曲线
分别为双曲线![]()
![]()
![]() 的左、右焦点,点P是以
的左、右焦点,点P是以![]() 为直径的圆与C在第一象限内的交点,若线段
为直径的圆与C在第一象限内的交点,若线段![]() 的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() (
(![]() )个单位长度后得到函数
)个单位长度后得到函数![]() 的图象,且函数
的图象,且函数![]() 的最大值为2.
的最大值为2.
(ⅰ)求函数![]() 的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数
的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某超市2018年12个月的收入与支出数据的折线图如图所示:

根据该折线图可知,下列说法错误的是( )
A. 该超市2018年的12个月中的7月份的收益最高
B. 该超市2018年的12个月中的4月份的收益最低
C. 该超市2018年1-6月份的总收益低于2018年7-12月份的总收益
D. 该超市2018年7-12月份的总收益比2018年1-6月份的总收益增长了90万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com