
【题目】
已知函数f(x)=![]() -bx+lnx(a,b∈R).
-bx+lnx(a,b∈R).
(Ⅰ)若a=b=1,求f(x)点(1,f(1))处的切线方程;
(Ⅱ)设a<0,求f(x)的单调区间;
(Ⅲ)设a<0,且对任意的x>0,f(x)≤f(2),试比较ln(-a)与-2b的大小.
【答案】(Ⅰ)![]() ;(Ⅱ)单调递增区间是
;(Ⅱ)单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
试题(Ⅰ)![]() 时,对函数求导,由导数的几何意义,可得切线的斜率
时,对函数求导,由导数的几何意义,可得切线的斜率![]() ,由点斜式可得切线方程
,由点斜式可得切线方程![]() ;(Ⅱ)对函数求导
;(Ⅱ)对函数求导![]() ,当
,当![]() 时,
时,![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() .显然,
.显然,![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,可得其单调区间;(Ⅲ)要比较ln(-a)与-2b的大小可用作差法,由(Ⅱ)知,
单调递减,可得其单调区间;(Ⅲ)要比较ln(-a)与-2b的大小可用作差法,由(Ⅱ)知,![]() 是
是![]() 的唯一的极大值点,由f(x)≤f(2),知函数
的唯一的极大值点,由f(x)≤f(2),知函数![]() 在
在![]() 处取得最大值,可得
处取得最大值,可得![]() ,即
,即![]() ,
,![]()
构造函数![]() ,求导可得
,求导可得![]() .令
.令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() 单调递减,
单调递减,![]() 是
是![]() 的最大值,即
的最大值,即![]() ≤
≤![]() ,进而得
,进而得![]() ,即证
,即证![]() .
.
试题解析:(Ⅰ)![]() 时,
时,![]() ,
,![]() , 1分
, 1分
∴![]() ,
,![]() , 2分
, 2分
故![]() 点
点![]() 处的切线方程是
处的切线方程是![]() . 3分
. 3分
(Ⅱ)由![]() ,得
,得![]() . 4分
. 4分
当![]() 时,
时,![]() ,得
,得![]() ,由
,由![]() ,
,
得![]() . 显然,
. 显然,![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
∴![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() . 8分
. 8分
(Ⅲ)由题意知函数![]() 在
在![]() 处取得最大值.由(Ⅱ)知,
处取得最大值.由(Ⅱ)知,![]() 是
是![]() 的唯一的极大值点,
的唯一的极大值点,
故![]() ,整理得
,整理得![]() . 9分
. 9分
于是![]()
令![]() ,则
,则![]() .令
.令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减. 10分
单调递减. 10分
因此对任意![]() ,
,![]() ≤
≤![]() ,又
,又![]() ,
,
故![]() ,即
,即![]() ,即
,即![]() ,
,
∴![]() . 12分
. 12分


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某中学根据学生的兴趣爱好,分别创建了“书法”、“诗词”、“理学”三个社团,据资料统计新生通过考核选拔进入这三个社团成功与否相互独立.2015年某新生入学,假设他通过考核选拔进入该校的“书法”、“诗词”、“理学”三个社团的概率依次为![]() 、
、![]() 、
、![]() ,己知三个社团他都能进入的概率为
,己知三个社团他都能进入的概率为![]() ,至少进入一个社团的概率为
,至少进入一个社团的概率为![]() ,且
,且![]() .
.
(1)求![]() 与
与![]() 的值;
的值;
(2)该校根据三个社团活动安排情况,对进入“书法”社的同学增加校本选修学分1分,对进入“诗词”社的同学增加校本选修学分2分,对进入“理学”社的同学增加校本选修学分3分.求该新同学在社团方面获得校本选修课学分分数不低于4分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为![]() 万元时,销售量
万元时,销售量![]() 万件满足
万件满足![]() (其中
(其中![]() ,
, ![]() 为正常数),现假定生产量与销售量相等,已知生产该产品
为正常数),现假定生产量与销售量相等,已知生产该产品![]() 万件还需投入成本
万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 万元/万件.
万元/万件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式。孪生素数猜想是希尔伯特在1900年提出的23个问题之一,可以这样描述:存在无穷多个素数p,使得p+2是素数,素数对(p,p+2)称为孪生素数.在不超过30的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线C:![]() 的左、右焦点为F1,F2,直线y
的左、右焦点为F1,F2,直线y![]() b与C的右支相交于点P,若|PF1|=2|PF2|,则双曲线C的离心率为_____;若该双曲线的焦点到其渐近线的距离是
b与C的右支相交于点P,若|PF1|=2|PF2|,则双曲线C的离心率为_____;若该双曲线的焦点到其渐近线的距离是![]() ,则双曲线的方程为_____.
,则双曲线的方程为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
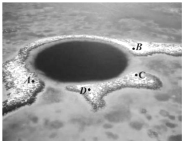
【题目】海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径![]() ,
,![]() 两点间的距离,现在珊瑚群岛上取两点
两点间的距离,现在珊瑚群岛上取两点![]() ,
,![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() 两点的距离为___.
两点的距离为___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为梯形,
为梯形, ![]() ,且
,且![]() ,
, ![]() 是边长为2的正三角形,顶点
是边长为2的正三角形,顶点![]() 在
在![]() 上的射影为点
上的射影为点![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.
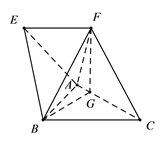
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆柱的轴截面![]() 是边长为2的正方形,点
是边长为2的正方形,点![]() 是圆弧
是圆弧![]() 上的一动点(不与
上的一动点(不与![]() 重合),点
重合),点![]() 是圆弧
是圆弧![]() 的中点,且点
的中点,且点![]() 在平面
在平面![]() 的两侧.
的两侧.
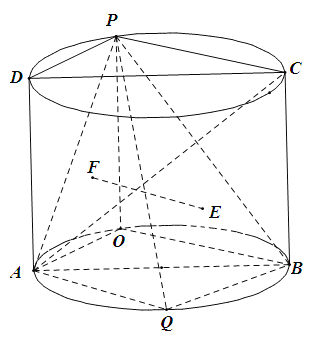
(1)证明:平面![]() 平面
平面![]() ;
;
(2)设点![]() 在平面
在平面![]() 上的射影为点
上的射影为点![]() ,点
,点![]() 分别是
分别是![]() 和
和![]() 的重心,当三棱锥
的重心,当三棱锥![]() 体积最大时,回答下列问题.
体积最大时,回答下列问题.
(ⅰ)证明:![]() 平面
平面![]() ;
;
(ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com