
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,若直线AB与a成角为60![]() ,则AB与b成角为
,则AB与b成角为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
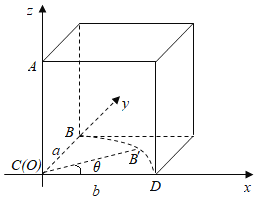
【解析】分析:由题意知,a、b、AC三条直线两两相互垂直,构建如图所示的边长为1的正方体,|AC|=1,|AB|=![]() ,斜边AB以直线AC为旋转轴,则A点保持不变,B点的运动轨迹是以C为圆心,1为半径的圆,以C坐标原点,以CD为x轴,CB为y轴,CA为z轴,建立空间直角坐标系,利用向量法能求出结果.
,斜边AB以直线AC为旋转轴,则A点保持不变,B点的运动轨迹是以C为圆心,1为半径的圆,以C坐标原点,以CD为x轴,CB为y轴,CA为z轴,建立空间直角坐标系,利用向量法能求出结果.
详解:由题意知,a、b、AC三条直线两两相互垂直,画出图形如图,
不妨设图中所示正方体边长为1,故|AC|=1,|AB|=![]() ,
,
斜边AB以直线AC为旋转轴,则A点保持不变,
B点的运动轨迹是以C为圆心,1为半径的圆,
以C坐标原点,以CD为x轴,CB为y轴,CA为z轴,建立空间直角坐标系,
则D(1,0,0),A(0,0,1),直线a的方向单位向量![]() =(0,1,0),|
=(0,1,0),|![]() |=1,
|=1,
直线b的方向单位向量![]() =(1,0,0),|
=(1,0,0),|![]() |=1,
|=1,
设B点在运动过程中的坐标中的坐标B′(cosθ,sinθ,0),
其中θ为B′C与CD的夹角,θ∈[0,2π),
∴AB′在运动过程中的向量,![]() =(cosθ,sinθ,﹣1),|
=(cosθ,sinθ,﹣1),|![]() |=
|=![]() ,
,
![]() 与
与![]() 所成夹角为β∈[0,
所成夹角为β∈[0,![]() ],
],
cosβ=![]() ,
,
当![]() 与
与![]() 夹角为60°时,即
夹角为60°时,即![]() ,
,
|sinθ|=![]() ,
,
∵cos2θ+sin2θ=1,∴cosβ=![]() |cosθ|=
|cosθ|=![]() ,
,
∵β∈[0,![]() ],∴β=
],∴β=![]() ,此时AB与b成角为60°.
,此时AB与b成角为60°.
故答案为:A


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(﹣∞,0)∪(0,+∞),f(x)是奇函数,且当x>0时,f(x)=x2﹣x+a,若函数g(x)=f(x)﹣x的零点恰有两个,则实数a的取值范围是( )
A.a<0B.a≤0C.a≤1D.a≤0或a=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,命题
,命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆,命题
轴上的椭圆,命题![]() 方程
方程![]() 表示双曲线.
表示双曲线.
(1)若命题![]() 是真命题,求实数
是真命题,求实数![]() 的范围;
的范围;
(2)若命题“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”是假命题,求实数
”是假命题,求实数![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )(参考数据:sin15°=0.2588,sin7.5°=0.1305)

A. 12B. 24C. 48D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切于点
相切于点![]() ,圆心
,圆心![]() 在
在![]() 轴上.
轴上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 分别与直线
分别与直线![]() 相交于
相交于![]() 两点,记
两点,记![]() ,
,![]() 的面积分别是
的面积分别是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() 且离心率为
且离心率为![]() .
.
(1)求椭圆C的方程;
(2)是否存在过点![]() 的直线
的直线![]() 与椭圆C相交于A,B两点,且满足
与椭圆C相交于A,B两点,且满足![]() .若存在,求出直线
.若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com