
 ij��λί��һ��������鹫˾�Ե�λ1000��Ա��������QQ�˶����ݵ��飬�������վ����߲�����ǧ������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��ÿ�����������˵㣬�������Ҷ˵㣬���һ���ʾ�˶�����[4��6��֮�䣨��λ��ǧ������
ij��λί��һ��������鹫˾�Ե�λ1000��Ա��������QQ�˶����ݵ��飬�������վ����߲�����ǧ������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��ÿ�����������˵㣬�������Ҷ˵㣬���һ���ʾ�˶�����[4��6��֮�䣨��λ��ǧ���������� ������Ƶ�ʷֲ�ֱ��ͼ�����λְ���վ����߲����ڣ�6��8����Ƶ�ʣ��ɴ��������λְԱ�վ����߲�����[6��8����������
������Ƶ�ʷֲ�ֱ��ͼ�������λ����
����������֪Ƿȱ�˶�����Ϊ��0.050+0.100����2��1000=300�ˣ������˶�Ⱥ�������Ϊ��0.075+0.025����2��1000=200�ˣ��÷ֲ�����ķ�����ȡ5�ˣ���Ƿȱ�˶�Ⱥ���ȡ3�ˣ������˶�Ⱥ���ȡ2 �ˣ��ɴ�����������˶�Ⱥ����������1��Ա���뽡�����ҽ����̸�ĸ��ʣ�
��� �⣺���������⼰Ƶ�ʷֲ�ֱ��ͼ֪����λְ���վ����߲����ڣ�6��8����Ƶ��Ϊ0.100��2=0.2��
�λְԱ�վ����߲�����[6��8��������Ϊ��0.2��1000=200�ˣ�
������Ƶ�ʷֲ�ֱ��ͼ����λ����[8��10���ڣ�
����λ��Ϊx��
��0.05��2+0.1��2+0.125����x-8��=0.5��
���x=9.6��
����������֪Ƿȱ�˶�����Ϊ��0.050+0.100����2��1000=300�ˣ�
�����˶�Ⱥ�������Ϊ��0.075+0.025����2��1000=200�ˣ�
�÷ֲ�����ķ�����ȡ5�ˣ�
��Ƿȱ�˶�Ⱥ���ȡ3�ˣ������˶�Ⱥ���ȡ2 �ˣ�
����5��Ա���������ȡ2���뽡�����ҽ����̸�������¼�����n=${C}_{5}^{2}=10$��
�����˶�Ⱥ����������1��Ա���뽡�����ҽ����̸�Ķ����¼��Ǵ�Ƿȱ�˶�Ⱥ���ȡ2���뽡�����ҽ����̸��
������˶�Ⱥ����������1��Ա���뽡�����ҽ����̸�ĸ���p=1-$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{7}{10}$��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ʵ������е��⣬����ʱҪ�������⣬ע������¼����ʼ��㹫ʽ�ĺ������ã�


 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
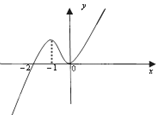 ��֪��R�Ͽɵ��ĺ���f��x����ͼ����ͼ��ʾ����ʽf��x��•f�䣨x����0�Ľ⼯Ϊ��������
��֪��R�Ͽɵ��ĺ���f��x����ͼ����ͼ��ʾ����ʽf��x��•f�䣨x����0�Ľ⼯Ϊ��������| A�� | ��-2��0�� | B�� | ��-�ޣ�-2���ȣ�-1��0�� | C�� | ��-�ޣ�-2���ȣ�0��+�ޣ� | D�� | ��-2��-1���ȣ�0��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��$\frac{3}{2}$�� | B�� | ��1��$\sqrt{2}$�� | C�� | ��$\sqrt{2}$��$\sqrt{3}$�� | D�� | ��$\sqrt{2}$��$\frac{3}{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-1��2+��y+3��2=2 | B�� | ��x+1��2+��y-3��2=4 | C�� | ��x-1��2+��y+3��2=4 | D�� | ��x+1��2+��y-3��2=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| �·�x | 1 | 2 | 3 | 4 |
| �õ���y | 4.5 | 4 | 3 | 2.5 |
| A�� | 5.1 | B�� | 4.8 | C�� | 5 | D�� | 5.2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{4}{3}$ | B�� | $\frac{5}{3}$ | C�� | $\frac{25}{9}$ | D�� | $\frac{16}{9}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com