
【题目】已知函数![]() ,
, ![]()
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若不等式![]() 的解集为空集,求实数
的解集为空集,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据绝对值内的零点去掉绝对值,将函数写成分段形式,分段解不等式即可;(2)根据题意将问题转化为2≤f(x)min,由绝对值三角不等式得到函数最值,求得参数范围即可。
解析:
(1)当a=3时,f(x)=|x﹣3|+|x﹣1|,
即有f(x)=
不等式f(x)≤4即为![]() 或
或![]() 或
或![]() .
.
即有0≤x<1或3≤x≤4或1≤x<3,则为0≤x≤4,
则解集为[0,4];
(2)依题意知,f(x)=|x﹣a|+|x﹣1|≥2恒成立,
∴2≤f(x)min;
由绝对值三角不等式得:f(x)=|x﹣a|+|x﹣1|≥|(x﹣a)+(1﹣x)|=|1﹣a|,
即f(x)min=|1﹣a|,
∴|1﹣a|≥2,即a﹣1≥2或a﹣1≤﹣2,
解得a≥3或a≤﹣1.
∴实数a的取值范围是[3,+∞)∪(﹣∞,﹣1].


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】某社区为了解辖区住户中离退休老人每天的平均户外“活动时间”,从辖区住户的离退休老人中随机抽取了100位老人进行调查,获得了每人每天的平均户外“活动时间”(单位:小时),活动时间按照![]() 、
、![]() 、…、
、…、![]() 从少到多分成9组,制成样本的频率分布直方图如图所示.
从少到多分成9组,制成样本的频率分布直方图如图所示.
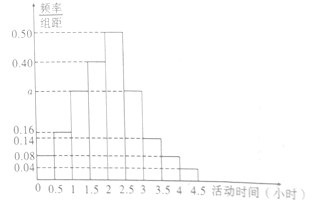
(1)求图中![]() 的值;
的值;
(2)估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数;
(3)在![]() 、
、![]() 这两组中采用分层抽样抽取7人,再从这7人中随机抽取2人,求抽取的两人恰好都在同一个组的概率.
这两组中采用分层抽样抽取7人,再从这7人中随机抽取2人,求抽取的两人恰好都在同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 是大于0的常数).以坐标原点为极点,
是大于0的常数).以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的极坐标方程和圆
的极坐标方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)分别记直线![]() :
: ![]() ,
, ![]() 与圆
与圆![]() 、圆
、圆![]() 的异于原点的焦点为
的异于原点的焦点为![]() ,
, ![]() ,若圆
,若圆![]() 与圆
与圆![]() 外切,试求实数
外切,试求实数![]() 的值及线段
的值及线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
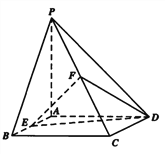
【题目】在四棱锥![]() 中,底面
中,底面![]() 是矩形,侧棱
是矩形,侧棱![]() 底面
底面![]() ,
, ![]() 分别是
分别是![]() 的中点,
的中点, ![]() ,
, ![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线y=t与曲线C:y=x(x﹣3)2的三个交点分别为A(a,t),B(b,t),C(c,t),且a<b<c.现给出如下结论:
①abc的取值范围是(0,4);
②a2+b2+c2为定值;③a+b+c=6
其中正确结论的为_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的![]() .现有3名工人独立地从中任选一个项目参与建设.
.现有3名工人独立地从中任选一个项目参与建设.
(1)求他们选择的项目所属类别互不相同的概率;
(2)记ξ为3人中选择的项目属于基础设施工程或产业建设工程的人数,求ξ的分布列及均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,直线
,直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知点![]() ,求证:若圆
,求证:若圆![]() 与直线
与直线![]() 相切,则圆
相切,则圆![]() 与直线
与直线![]() 也相切.
也相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)和y=g(x)在[-2,2]上的图象如图所示.给出下列四个命题:
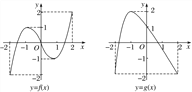
①方程f[g(x)]=0有且仅有6个根;②方程g[f(x)]=0有且仅有3个根;
③方程f[f(x)]=0有且仅有7个根;④方程g[g(x)]=0有且仅有4个根.
其中正确命题的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com