
【题目】已知点 ![]() ,点P是圆
,点P是圆 ![]() 上的任意一点,设Q为该圆的圆心,并且线段PA的垂直平分线与直线PQ交于点E.
上的任意一点,设Q为该圆的圆心,并且线段PA的垂直平分线与直线PQ交于点E.
(1)求点E的轨迹方程;
(2)已知M,N两点的坐标分别为(﹣2,0),(2,0),点T是直线x=4上的一个动点,且直线TM,TN分别交(1)中点E的轨迹于C,D两点(M,N,C,D四点互不相同),证明:直线CD恒过一定点,并求出该定点坐标.
【答案】
(1)解:∵|EA|+|QE|=|EQ|+|PE|=4,且|QA|=2 ![]() <4,
<4,
∴点E的轨迹是以A,Q为焦点的椭圆,
设椭圆方程为 ![]() =1,则2a=4,c=
=1,则2a=4,c= ![]() ,∴a=2,b=
,∴a=2,b= ![]() =1.
=1.
所以点E的轨迹方程为: ![]()
(2)解:依题意设直线CD的方程为:x=my+n,
代入椭圆方程x2+4y2=4得:(4+m2)y2+2mny+(n2﹣4)=0
设C(x1,y1),D(x2,y2),则 ![]() ,
, ![]() .
.
∵直线TM方程为 ![]() ,直线TN方程为
,直线TN方程为 ![]() ,
,
由题知TM,TN的交点T的横坐标为4,∴ ![]() ,即3y1(x2﹣2)=y2(x1+2),
,即3y1(x2﹣2)=y2(x1+2),
即:3y1(my2+n﹣2)=y2(my1+n+2),整理得:2my1y2=(n+2)y2﹣3(n﹣2)y1,
∴ ![]()
化简可得: ![]() .
.
∵当m,y1变化时,上式恒成立,∴n=1,
∴直线CD恒过一定点(1,0)
【解析】(1)利用椭圆的定义即可得出E的轨迹方程;(2)设CD方程x=my+n,代入椭圆方程消元,得出C,D坐标的关系,求出TM,TN的方程,根据交点横坐标为4得出恒等式,从而得出n的值,即得出直线CD的定点坐标.


科目:高中数学 来源: 题型:
【题目】已知椭圆C的对称中心为原点O,焦点在x轴上,离心率为![]() ,且点
,且点![]() 在该椭圆上。
在该椭圆上。
(I)求椭圆C的方程;
(II)过椭圆C的左焦点![]() 的直线l与椭圆C相交于
的直线l与椭圆C相交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求圆心在原点O且与直线l相切的圆的方程。
,求圆心在原点O且与直线l相切的圆的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年我国将加快阶梯水价推行,原则是“保基本、建机制、促节约”,其中“保基本”是指保证至少80%的居民用户用水价格不变.为响应国家政策,制定合理的阶梯用水价格,某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研,抽取的数据的茎叶图如下(单位:吨):

(1)在郊区的这5户居民中随机抽取2户,求其年人均用水量都不超过30吨的概率;
(2)设该城市郊区和城区的居民户数比为![]() ,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,并保证这一梯次的居民用户用水价格保持不变.试根据样本估计总体的思想,分析此方案是否符合国家“保基本”政策.
,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,并保证这一梯次的居民用户用水价格保持不变.试根据样本估计总体的思想,分析此方案是否符合国家“保基本”政策.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较注射![]() 两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,毎组100只,其中一组注射药物
两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,毎组100只,其中一组注射药物![]() ,另一组注射药物
,另一组注射药物![]() .
.
(1)甲、乙是200只家兔中的2只,求甲、乙分在不同组的概率;
(2)下表1和表2分别是注射药物![]() 和
和![]() 后的试验结果.(疱疹面积单位:
后的试验结果.(疱疹面积单位: ![]() )
)
表1:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表

表2:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表

(ⅰ)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
(ⅱ)完成下面![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“注射药物
的把握认为“注射药物![]() 后的疱疹面积与注射药物
后的疱疹面积与注射药物![]() 后的疱疹面积有差异”.
后的疱疹面积有差异”.
表3:

附: 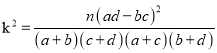
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点![]() 为圆心的圆经过点
为圆心的圆经过点![]() 和
和![]() ,线段
,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 于点
于点![]() 和
和![]() ,且
,且![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)求圆![]() 的方程;
的方程;
(3)设点![]() 在圆
在圆![]() 上,试问使△
上,试问使△![]() 的面积等于8的点
的面积等于8的点![]() 共有几个?证明你的结论.
共有几个?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 上异于长轴端点的两点.
上异于长轴端点的两点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() :
: ![]() ,且
,且![]() ,垂足为
,垂足为![]() ,
, ![]() ,垂足为
,垂足为![]() ,若
,若![]() ,且
,且![]() 的面积是
的面积是![]() 面积的5倍,求
面积的5倍,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足 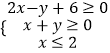 ,若目标函数z=﹣mx+y的最大值为﹣2m+10,最小值为﹣2m﹣2,则实数m的取值范围是( )
,若目标函数z=﹣mx+y的最大值为﹣2m+10,最小值为﹣2m﹣2,则实数m的取值范围是( )
A.[﹣1,2]
B.[﹣2,1]
C.[2,3]
D.[﹣1,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com