
(本小题满分16分)
设函数 (其中常数
(其中常数 >0,且
>0,且 ≠1).
≠1).
(Ⅰ)当 时,解关于
时,解关于 的方程
的方程 (其中常数
(其中常数 );
);
(Ⅱ)若函数 在
在 上的最小值是一个与
上的最小值是一个与 无关的常数,求实数
无关的常数,求实数 的取值范围.
的取值范围.
(1)x=lg.
(2)当a≥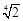 时,f(x)在(-∞,2]上的最小值与a无关
时,f(x)在(-∞,2]上的最小值与a无关
【解析】解
(Ⅰ)f(x)=
① 当x<0时,f(x)=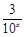 >3.因为m>2.则当2<m≤3时,方程f(x)=m无解;
>3.因为m>2.则当2<m≤3时,方程f(x)=m无解;
当m>3,由10x=,得x=lg. …………………… 1分
② 当x≥0时,10x≥1.由f(x)=m得10x+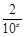 =m,∴(10x)2-m10x+2=0.
=m,∴(10x)2-m10x+2=0.
因为m>2,判别式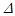 =m2-8>0,解得10x=. …………………… 3分
=m2-8>0,解得10x=. …………………… 3分
因为m>2,所以>>1.所以由10x=,解得x=lg.
令=1,得m=3. …………………… 4分
所以当m>3时,=<=1,
当2<m≤3时,=>=1,解得x=lg .…………… 5分
综上,当m>3时,方程f(x)=m有两解x=lg 和x=lg ;
当2<m≤3时,方程f(x)=m有两解x=lg .…………………… 6分
(2) (Ⅰ)若0<a<1,当x<0时,0<f(x)=<3;当0≤x≤2时,f(x)=ax+.… 7分
令t=ax,则t∈[a2,1],g(t)=t+在[a2,1]上单调递减,所以当t=1,即x=0时f(x)取得最小值为3.
当t=a2时,f(x)取得最大值为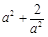 .此时f(x)在(-∞,2]上的值域是(0,
.此时f(x)在(-∞,2]上的值域是(0,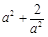 ],没有最小值.…………………………… 9分
],没有最小值.…………………………… 9分
(Ⅱ)若a>1,当x<0时,f(x)=>3;当0≤x≤2时f(x)=ax+.
令t=ax,g(t)=t+,则t∈[1,a2].
① 若a2≤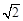 ,g(t)=t+在[1,a2]上单调递减,所以当t=a2即x=2时f(x)取最小值a2+,最小值与a有关;…………………………… 11分
,g(t)=t+在[1,a2]上单调递减,所以当t=a2即x=2时f(x)取最小值a2+,最小值与a有关;…………………………… 11分
② a2≥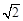 ,g(t)=t+在[1,]上单调递减,在[,a2]上单调递增,…………13分
,g(t)=t+在[1,]上单调递减,在[,a2]上单调递增,…………13分
所以当t=即x=loga时f(x)取最小值2,最小值与a无关.……………… 15分
综上所述,当a≥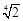 时,f(x)在(-∞,2]上的最小值与a无关.……………………… 16分
时,f(x)在(-∞,2]上的最小值与a无关.……………………… 16分


科目:高中数学 来源: 题型:
(2010江苏卷)18、(本小题满分16分)
 在平面直角坐标系
在平面直角坐标系![]() 中,如图,已知椭圆
中,如图,已知椭圆![]() 的左、右顶点为A、B,右焦点为F。设过点T(
的左、右顶点为A、B,右焦点为F。设过点T(![]() )的直线TA、TB与椭圆分别交于点M
)的直线TA、TB与椭圆分别交于点M![]() 、
、![]() ,其中m>0,
,其中m>0,![]() 。
。
(1)设动点P满足![]() ,求点P的轨迹;
,求点P的轨迹;
(2)设![]() ,求点T的坐标;
,求点T的坐标;
(3)设![]() ,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
查看答案和解析>>
科目:高中数学 来源:2010年泰州中学高一下学期期末测试数学 题型:解答题
(本小题满分16分)
函数 ,
, (
( ),
),
A=
(Ⅰ)求集合A;
(Ⅱ)如果 ,对任意
,对任意 时,
时, 恒成立,求实数
恒成立,求实数 的范围;
的范围;
(Ⅲ)如果 ,当“
,当“ 对任意
对任意 恒成立”与“
恒成立”与“ 在
在 内必有解”同时成立时,求
内必有解”同时成立时,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2014届江苏大丰新丰中学高二上期中考试文数学试卷(解析版) 题型:解答题
(本小题满分16分) 本题请注意换算单位
某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米。已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元。
(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;
(总开发费用=总建筑费用+购地费用)
(2)要使整幢写字楼每平方米开发费用最低,该写字楼应建为多少层?
查看答案和解析>>
科目:高中数学 来源:2013届安徽省蚌埠市高二下学期期中联考文科数学试卷(解析版) 题型:解答题
(本小题满分16分)设命题 :方程
:方程 无实数根;
命题
无实数根;
命题 :函数
:函数
 的值域是
的值域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010年江苏省高一第三阶段检测数学卷 题型:解答题
(本小题满分16分)
已知函数f(x)= 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(Ⅰ)求f( )的值;
)的值;
(Ⅱ)将函数y=f(x)的图象向右平移 个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com