(1)一次函数f(x)=kx+h(k≠0),若m<n有f(m)>0,f(n)>0,则对于任意x∈(m,n)都有f(x)>0,试证明之;
(2)试用上面结论证明下面的命题:若a,b,c∈R且|a|<1,|b|<1,|c|<1,则ab+bc+ca>-1.
解:(1)证明:
当k>0时,函数f(x)=kx+h在x∈R上是增函数,
m<x<n,f(x)>f(m)>0;
当k<0时,函数f(x)=kx+h在x∈R上是减函数,
m<x<n,f(x)>f(n)>0.
所以对于任意x∈(m,n)
都有f(x)>0成立.
(2)将ab+bc+ca+1写成(b+c)a+bc+1
,构造函数f(x)=(b+c)x+bc+1.
则f(a)=(b+c)a+bc+1.
当b+c=0时,即b=-c,
f(a)=bc+1=-c2+1.
因为|c|<1,
所以f(a)=-c2+1>0.
当b+c≠0时,
f(x)=(b+c)x+bc+1为x的一次函数.
因为|b|<1,|c|<1,
f(1)=b+c+bc+1=(1+b)(1+c)>0,
f(-1)=-b-c+bc+1=(1-b)(1-c)>0.
由问题(1)对于|a|<1的一切值f(a)>0,
即(b+c)a+bc+1=ab+ac+bc+1>0.
分析:(1)实质上是要证明,一次函数f(x)=kx+h(k≠0),x∈(m,n).若区间两个端点的函数值均为正,则对于任意x∈(m,n)都有f(x)>0.之所以具有上述性质是由于一次函数是单调的.因此本问题的证明要从函数单调性入手.
(2)在(1)的结论下,构造函数f(x)=(b+c)x+bc+1.然后对b+c进行分析,分情况进行讨论,最后综合两种情况证明ab+bc+ca>-1.
点评:本题为不等式的证明,通过对一次函数单调性的考查,分别证明f(x)>0成立.然后在(1)的条件下加入一些条件继续证明.本题考查对函数性质的灵活掌握和运用,以及对函数单调性的熟练运用.



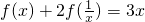 ,求f(x)的表达式.
,求f(x)的表达式. ,求f(x)的表达式.
,求f(x)的表达式.