【题目】下列说法中正确的个数是（ ）
①球的半径是球面上任意一点与对球心的连线；
②球面上任意两点的连线是球的直径；
③用一个平面截一个球，得到的截面是一个圆；
④用一个平面截一个球，得到的截面是一个圆面；
⑤以半圆的直径所在直线为轴旋转形成的曲面叫做球；
⑥空间中到定点的距离等于定长的所有的点构成的曲面是球面.
A.0B.1C.2D.3
科目：高中数学 来源： 题型：
【题目】某企业欲做一个介绍企业发展史的铭牌，铭牌的截面形状是如图所示的扇形环面(由扇形
挖去扇形
后构成的)．已知
，线段
与弧
、弧
的长度之和为
米，圆心角为
弧度．
(1)求关于
的函数解析式；
(2)记铭牌的截面面积为
，试问取何值时，的值最大？并求出最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2018年央视大型文化节目《经典咏流传》的热播，在全民中掀起了诵读诗词的热潮.某大学社团调查了该校文学院300名学生每天诵读诗词的时间(所有学生诵读时间都在两小时内)，并按时间(单位：分钟)将学生分成六个组：
，
，
，
，
，
，经统计得到了如图所
示的频率分布直方图
(Ⅰ)求频率分布直方图中
的值，并估计该校文学院的学生每天诵读诗词的时间的平均数；
(Ⅱ)若两个同学诵读诗词的时间
满足
，则这两个同学组成一个“Team”，已知从每天诵读时间小于20分钟和大于或等于80分钟的所有学生中用分层抽样的方法抽取了5人，现从这5人中随机选取2人，求选取的两人能组成一个“Team”的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，已知倾斜角为α的直线l过点A（2，1）．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系曲线C的极坐标方程为ρ＝2sinθ，直线l与曲线C分别交于P，Q两点．
（1）写出直线l的参数方程和曲线C的直角坐标方程．
（2）求｜AP｜｜AQ｜的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】有下列4个命题：
（1）“若
，则
互为相反数”的否命题
（2）“若
，则
”的逆否命题
（3）“若
，则
”的否命题
（4）“若
，则
有实数根”的逆命题
其中真命题的个数是（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（多选题）有下列几个命题，其中正确的命题是（ ）
A.函数
在
上是增函数
B.函数
在
上是减函数
C.函数
的单调区间是
D.已知
在
上是增函数，若
，则有
E.已知函数
是奇函数，则
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某大风车的半径为2米，每12秒旋转一周，它的最低点O离地面1米，点O在地面上的射影为A.风车圆周上一点M从最低点O开始，逆时针方向旋转40秒后到达P点，则点P到点A的距离与点P的高度之和为（ ）
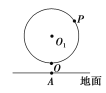
A. 5米B. (4＋
)米
C. (4＋
)米D. (4＋
)米
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业生产的一种电器的固定成本（即固定投资）为0.5万元，每生产一台这种电器还需可变成本（即另增加投资）25元，市场对这种电器的年需求量为5百台.已知这种电器的销售收入R与销售量t的关系可用抛物线表示，如图.
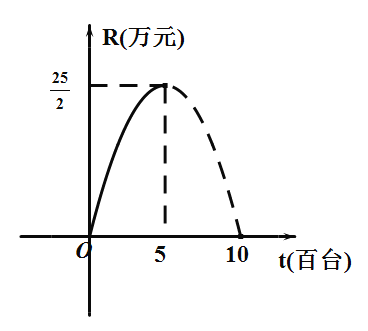
（注：销售量的单位：百台，销售收入与纯收益的单位：万元，生产成本=固定成本+可变成本，精确到1台和0.01万元）
（1）写出销售收入R与销售量t之间的函数关系式；
（2）若销售收入减去生产成本为纯收益，写出纯收益与销售量的函数关系式，并求销售量是多少时，纯收益最大.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）当
时，求函数
图象在点
处的切线方程；
（2）当
时，讨论函数的单调性
（3）是否存在实数
，对任意的
有
恒成立？若存在，求出的取值范围:若不存在，说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
