
【题目】已知f(x)=2x2+bx+c.
(1)对任意x∈[﹣1,1],f(x)的最大值与最小值之差不大于6,求b的取值范围;
(2)若f(x)=0有两个不同实根,f(f(x))无零点,求证: ![]() ﹣
﹣ ![]() >1.
>1.
【答案】
(1)解:f(x)=2x2+bx+c= ![]() +c﹣
+c﹣ ![]() ,x∈[﹣1,1].
,x∈[﹣1,1].
①当﹣ ![]() ≤﹣1,即b≥4时,函数f(x)在x∈[﹣1,1]单调递增,∴f(1)﹣f(﹣1)≤6,化为:b≤3,舍去;
≤﹣1,即b≥4时,函数f(x)在x∈[﹣1,1]单调递增,∴f(1)﹣f(﹣1)≤6,化为:b≤3,舍去;
②当﹣ ![]() ≥1,即b≤﹣4时,函数f(x)在x∈[﹣1,1]单调递减,∴f(﹣1)﹣f(1)≤6,化为:b≥﹣3,舍去;
≥1,即b≤﹣4时,函数f(x)在x∈[﹣1,1]单调递减,∴f(﹣1)﹣f(1)≤6,化为:b≥﹣3,舍去;
③当﹣1<﹣ ![]() <1,即﹣4<b<4时,函数f(x)在
<1,即﹣4<b<4时,函数f(x)在 ![]() 内单调递减,在
内单调递减,在 ![]() 内单调递增,∴f(x)min=c﹣
内单调递增,∴f(x)min=c﹣ ![]() .
.
∵f(1)﹣f(﹣1)=2b,当0≤b<4时,f(x)max=f(1)=2+b+c,则2+b+c﹣ ![]() ≤6,解得0≤b≤
≤6,解得0≤b≤ ![]() .
.
当﹣4<b<0时,f(x)max=f(﹣1)=2﹣b+c,则2﹣b+c﹣ ![]() ≤6,解得
≤6,解得 ![]() ≤b<0.
≤b<0.
综上可得:b的取值范围是 ![]()
(2)证明:f(x)=2x2+bx+c=0有两个不同实根,∴△=b2﹣8c>0.
可得此方程的两个实数根:x1= ![]() ,x2=
,x2= ![]() .
.
要使f(f(x))无零点,则方程f(x)=x1,f(x)=x2,均无解.
∵x1>x2,∴f(x)=2x2+bx+c的最小值c﹣ ![]() >x1=
>x1= ![]() ,即b2﹣8c+2
,即b2﹣8c+2 ![]() +1<2b+1,
+1<2b+1,
∴ ![]() <2b+1,∴
<2b+1,∴ ![]() +1<
+1< ![]() .
.
∴ ![]() ﹣
﹣ ![]() >1
>1
【解析】(1)f(x)=2x2+bx+c= ![]() +c﹣
+c﹣ ![]() ,x∈[﹣1,1].对b分类讨论,利用二次函数的单调性即可得出.(2)f(x)=2x2+bx+c=0有两个不同实根,可得△>0.可得此方程的两个实数根:x1=
,x∈[﹣1,1].对b分类讨论,利用二次函数的单调性即可得出.(2)f(x)=2x2+bx+c=0有两个不同实根,可得△>0.可得此方程的两个实数根:x1= ![]() ,x2=
,x2= ![]() .要使f(f(x))无零点,则方程f(x)=x1 , f(x)=x2 , 均无解.由于x1>x2 , 可得f(x)=2x2+bx+c的最小值c﹣
.要使f(f(x))无零点,则方程f(x)=x1 , f(x)=x2 , 均无解.由于x1>x2 , 可得f(x)=2x2+bx+c的最小值c﹣ ![]() >x1 , 化简整理即可证明.
>x1 , 化简整理即可证明.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
【题目】为了了解初三女生身高情况,某中学对初三女生身高情况进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合 计 | M | N |
(1)求出表中m,n,M,N所表示的数分别是多少?
(2)画出频率分布直方图;
(3)全体女生中身高在哪组范围内的人数最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个顶点A(m,n)、B(2,1)、C(﹣2,3);
(1)求BC边所在直线的方程;
(2)BC边上中线AD的方程为2x﹣3y+6=0,且S△ABC=7,求点A的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
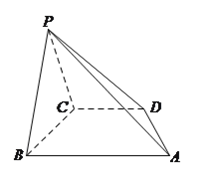
【题目】在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)求平面![]() 和平面
和平面![]() 所成二面角(小于
所成二面角(小于![]() )的大小.
)的大小.
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() 使得
使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张老师开车上班,有路线①与路线②两条路线可供选择. 路线①:沿途有![]() 两处独立运行的交通信号灯,且两处遇到绿灯的概率依次为
两处独立运行的交通信号灯,且两处遇到绿灯的概率依次为![]() ,若
,若![]() 处遇红灯或黄灯,则导致延误时间2分钟;若
处遇红灯或黄灯,则导致延误时间2分钟;若![]() 处遇红灯或黄灯,则导致延误时间3分钟;若两处都遇绿灯,则全程所花时间为20分钟.
处遇红灯或黄灯,则导致延误时间3分钟;若两处都遇绿灯,则全程所花时间为20分钟.
路线②:沿途有![]() 两处独立运行的交通信号灯,且两处遇到绿灯的概率依次为
两处独立运行的交通信号灯,且两处遇到绿灯的概率依次为![]() ,若
,若![]() 处遇红灯或黄灯,则导致延误时间8分钟;若
处遇红灯或黄灯,则导致延误时间8分钟;若![]() 处遇红灯或黄灯,则导致延误时间5分钟;若两处都遇绿灯,则全程所花时间为15分钟.
处遇红灯或黄灯,则导致延误时间5分钟;若两处都遇绿灯,则全程所花时间为15分钟.
(1)若张老师选择路线①,求他20分钟能到校的概率;
(2)为使张老师日常上班途中所花时间较少,你建议张老师选择哪条路线?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com