
(本小题满分1 4分)已知m,t∈R,函数f (x) =(x - t)3+m.
(I)当t =1时,
(i)若f (1) =1,求函数f (x)的单调区间;
(ii)若关于x的不等式f (x)≥x3—1在区间[1,2]上有解,求m的取值范围;
(Ⅱ)已知曲线y= f (x)在其图象上的两点A(x1,f (x1)),B(x2,f (x2)))( x1≠x2)处的切线
分别为l1、l2.若直线l1与l2平行,试探究点A与点B的关系,并证明你的结论.
解:(Ⅰ)(i)因为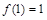 ,所以
,所以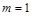 ,·················· 1分
,·················· 1分
则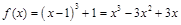 ,
而
,
而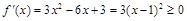 恒成立,
恒成立,
所以函数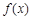 的单调递增区间为
的单调递增区间为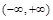 .·············· 4分
.·············· 4分
(ii)不等式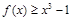 在区间
在区间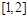 上有解,
上有解,
即 不等式 在区间
在区间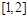 上有解,
上有解,
即 不等式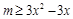 在区间
在区间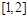 上有解,
上有解,
等价于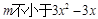 在区间
在区间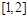 上的最小值,············· 6分
上的最小值,············· 6分
因为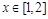 时,
时,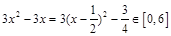 ,
,
所以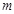 的取值范围是
的取值范围是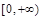 .···················· 9分
.···················· 9分
(Ⅱ)因为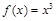 的对称中心为
的对称中心为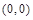 ,
,
而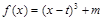 可以由
可以由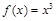 经平移得到,
经平移得到,
所以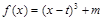 的对称中心为
的对称中心为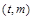 ,故合情猜测,若直线
,故合情猜测,若直线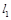 与
与 平行,则点
平行,则点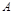 与点
与点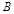 关于点
关于点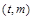 对称. 10分
对称. 10分
对猜想证明如下:
因为
所以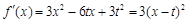
所以,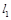 ,
, 的斜率分别为
的斜率分别为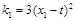 ,
,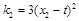 .
.
又直线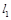 与
与 平行,所以
平行,所以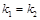 ,即
,即 ,
,
因为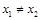 ,
,
所以,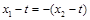 ,························ 12分
,························ 12分
从而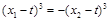 ,
,
所以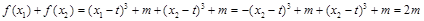 .
.
又由上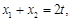
所以点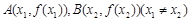 关于点(
关于点(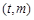 对称.
对称.
故直线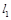 与
与 平行时,点
平行时,点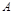 与点
与点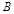 关于点
关于点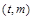 对称.·········· 14分
对称.·········· 14分
【解析】略


科目:高中数学 来源:2013年全国普通高等学校招生统一考试文科数学(新课标1卷解析版) 题型:解答题
(本小题满分共12分)为了比较两种治疗失眠症的药(分别成为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位:h)实验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5

(1)分别计算两组数据的平均数,从计算结果来看,哪种药的效果好?
(2)完成茎叶图,从茎叶图来看,哪种药疗效更好?
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省潍坊市高三3月第一次模拟考试文科数学试卷(解析版) 题型:解答题
(本小题满分1 2分)
如图,四边形ABCD中,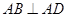 ,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD
,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD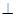 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.
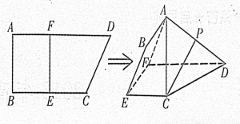
( I )当E为BC中点时,求证:CP//平面ABEF
(Ⅱ)设BE=x,问当x为何值时,三棱锥A-CDF的体积有最大值?并求出这个最大值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三质量检测理科数学 题型:解答题
(本小题满分1 3分)
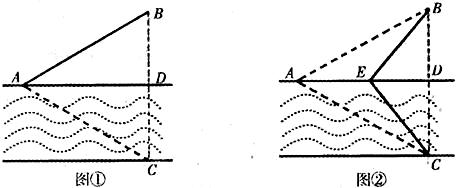
如图①,一条宽为l km的两平行河岸有村庄A和供电站C,村庄B与A、C的直线距离都是2km,BC与河岸垂直,垂足为D.现要修建电缆,从供电站C向村庄A、B供电.修建地下电缆、水下电缆的费用分别是2万元/km、4万元/km.
(Ⅰ)已知村庄A与B原来铺设有旧电缆仰,需要改造,旧电缆的改造费用是0.5万元/km.现
决定利用旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值.
(Ⅱ)如图②,点E在线段AD上,且铺设电缆的线路为CE、EA、EB.若∠DCE=θ (0≤θ≤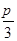 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三第一学期期末质量检测理科数学 题型:解答题
(本小题满分1
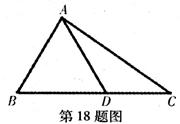
3分)如图,在△ABC中,已知B=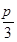 ,AC=4
,AC=4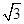 ,D为BC边上一点.
,D为BC边上一点.
(I)若AD=2,S△ABC=2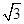 ,求DC的长;
,求DC的长;
(Ⅱ)若AB=AD,试求△ADC的周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com