
【题目】已知两定点![]() ,点
,点![]() 是平面内的动点,且
是平面内的动点,且![]() ,记
,记![]() 的轨迹是
的轨迹是![]()
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 引直线
引直线![]() 交曲线
交曲线![]() 于
于![]() 两点,设
两点,设![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明直线
,证明直线![]() 过定点.
过定点.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
设![]() ,根据条件列方程化简即可;(2)先探究特殊性,当点Q为椭圆的上顶
,根据条件列方程化简即可;(2)先探究特殊性,当点Q为椭圆的上顶
点(0,![]() )时,直线RN过定点P(4,0).再讨论一般情形,设直线l:
)时,直线RN过定点P(4,0).再讨论一般情形,设直线l:![]() 点R,N,P三点共线,因此直线RN经过定点P(4,0).
点R,N,P三点共线,因此直线RN经过定点P(4,0).
(1)设![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
由于![]() ,
,
即![]() ,设
,设![]() ,
,![]() ,
,
则![]() ,点
,点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点的椭圆,
为焦点的椭圆,
故![]() ,
,![]() ,
,![]() ,
,
所以,动点![]() 的轨迹
的轨迹![]() 的方程为:
的方程为:![]() .
.
如图所示,

先探究特殊性,当点Q为椭圆的上顶点(0,![]() )时,直线l:
)时,直线l:![]() ,
,
联立直线和椭圆方程得![]() ,
,
![]() 直线RN:
直线RN:![]() 令y=0,得x=4,
令y=0,得x=4,
所以直线RN过定点P(4,0).
下面证明一般情形:
设直线l:![]()
联立![]() ,
,
判别式![]()
所以![]()
![]()
即![]() ,
,
设![]() ,于是,
,于是,
 ,
,
又![]() ,
,
解得![]() ,
,
所以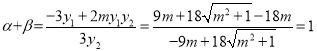 ,
,
所以点R,N,P三点共线,因此直线RN经过定点P(4,0).
综上,直线RN经过定点P(4,0).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为降低空气污染,提高环境质量,政府决定对汽车尾气进行整治.某厂家生产甲、乙两种不同型号的汽车尾气净化器,为保证净化器的质量,分别从甲、乙两种型号的净化器中随机抽取100件作为样本进行产品性能质量评估,评估综合得分![]() 都在区间
都在区间![]() .已知评估综合得分与产品等级如下表:
.已知评估综合得分与产品等级如下表:

根据评估综合得分,统计整理得到了甲型号的样本频数分布表和乙型号的样本频率分布直方图(图表如下).


甲型 乙型
(Ⅰ)从厂家生产的乙型净化器中随机抽取一件,估计这件产品为二级品的概率;
(Ⅱ)从厂家生产的乙型净化器中随机抽取3件,设随机变量![]() 为其中二级品的个数,求
为其中二级品的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)根据图表数据,请自定标准,对甲、乙两种型号汽车尾气净化器的优劣情况进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( ).
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.

A. 互联网行业从业人员中90后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的20%
C. 互联网行业中从事运营岗位的人数90后比80前多
D. 互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为坐标原点,点
为坐标原点,点![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)圆![]() 是以
是以![]() 为直径的圆,一直线
为直径的圆,一直线![]() 与圆
与圆![]() 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点![]() 、
、![]() ,当
,当![]() ,且满足
,且满足![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com