
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)给出![]() 的一个取值,使得曲线
的一个取值,使得曲线![]() 存在斜率为
存在斜率为![]() 的切线,并说明理由;
的切线,并说明理由;
(Ⅱ)若![]() 存在极小值和极大值,证明:
存在极小值和极大值,证明: ![]() 的极小值大于极大值.
的极小值大于极大值.
【答案】(I)详见解析;(II)详见解析.
【解析】试题分析:(Ⅰ)先对原函数求导,只需令方程![]() 有解即可得
有解即可得![]() 的范围,进而可得
的范围,进而可得![]() 的一个取值,在验证即可;(Ⅱ)对
的一个取值,在验证即可;(Ⅱ)对![]() 求导;求方程
求导;求方程![]() 的所有实数根,列表格判断各个根左右两边符合。进而可得结果.
的所有实数根,列表格判断各个根左右两边符合。进而可得结果.
试题解析:(Ⅰ)函数![]() 的定义域是
的定义域是![]() 且
且![]() ,且
,且![]() .
.
当![]() 时,曲线
时,曲线![]() 存在斜率为
存在斜率为![]() 的切线.证明如下:
的切线.证明如下:
曲线![]() 存在斜率为
存在斜率为![]() 的切线
的切线![]() 方程
方程![]() 存在
存在![]() 上的解,
上的解,
令![]() ,整理得
,整理得![]() ,
,
解得![]() ,或
,或![]() .
.
所以,当![]() 时,曲线
时,曲线![]() 存在斜率为
存在斜率为![]() 的切线.
的切线.
注:本题答案不唯一,只要![]() 均符合要求.
均符合要求.
(Ⅱ)由(Ⅰ)得![]() .
.
①当![]() 时,
时, ![]() 恒成立,
恒成立,
函数![]() 在区间
在区间![]() 和
和![]() 上单调递增,无极值,不合题意.
上单调递增,无极值,不合题意.
②当![]() 时,令
时,令![]() ,整理得
,整理得![]() .
.
由![]() ,
,
所以,上述方程必有两个不相等的实数解![]() ,
, ![]() ,不妨设
,不妨设![]() .
.
由![]() 得
得![]() .
.
![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
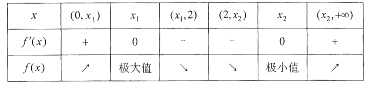
所以, ![]() 存在极大值
存在极大值![]() ,极小值
,极小值![]() .
.
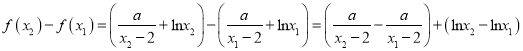 .
.
因为![]() ,且
,且![]() .
.
所以![]() ,
, ![]() ,
,
所以![]() .
.
所以![]() 的极小值大于极大值.
的极小值大于极大值.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】漳州水仙鳞茎硕大,箭多花繁,色美香郁,素雅娟丽,有“天下水仙数漳州”之美誉.现某水仙花雕刻师受雇每天雕刻250粒水仙花,雕刻师每雕刻一粒可赚1.2元,如果雕刻师当天超额完成任务,则超出的部分每粒多赚0.5元;如果当天未能按量完成任务,则按完成的雕刻量领取当天工资.
(Ⅰ)求雕刻师当天收入(单位:元)关于雕刻量![]() (单位:粒,
(单位:粒, ![]() )的函数解析式
)的函数解析式![]() ;
;
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量![]() (单位:粒),整理得下表:
(单位:粒),整理得下表:
雕刻量 | 210 | 230 | 250 | 270 | 300 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10天记录的各雕刻量的频率作为各雕刻量发生的概率.
(ⅰ)求该雕刻师这10天的平均收入;
(ⅱ)求该雕刻师当天的收入不低于300元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 上一点,平面
上一点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.

(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)若![]() ,试问平面
,试问平面![]() 是否可能与平面
是否可能与平面![]() 垂直?若能,求出
垂直?若能,求出![]() 值;若不能,说明理由。
值;若不能,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1 000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)请分析函数y= ![]() +1是否符合公司要求的奖励函数模型,并说明原因;
+1是否符合公司要求的奖励函数模型,并说明原因;
(2)若该公司采用函数模型y= ![]() 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 是过点
是过点![]() ,倾斜角为
,倾斜角为![]() 的直线,以直角坐标系
的直线,以直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的一个参数方程;
的一个参数方程;
(2)曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学一位高三班主任对本班50名学生学习积极性和对班级工作的态度进行调查, 得倒的统计数据如表所示:
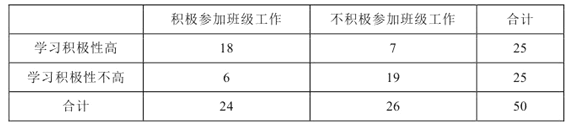
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作的且学习积极性高的7名学生中有两名男生,现从中抽取2名学生参加某项活动,问2名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.

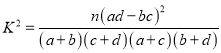
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com