
【题目】下列关于函数![]() 的判断正确的是( )
的判断正确的是( )
①![]() 的解集是
的解集是![]() ;
;
②![]() 极小值,
极小值,![]() 是极大值;
是极大值;
③![]() 没有最小值,也没有最大值.
没有最小值,也没有最大值.
A. ①③ B. ①②③ C. ② D. ①②
【答案】D
【解析】分析:由f(x)>0可解得x的范围,从而确定①正确;
对函数f(x)进行求导,然后令f'(x)=0求出x,在根据f'(x)的正负判断原函数的单调性进而可确定②正确.
根据函数的单调性可判断极大值即是原函数的最大值,无最小值,③不正确.从而得到答案.
详解:由f(x)>0(2x﹣x2)ex>02x﹣x2>00<x<2,故①正确;
f′(x)=ex(2﹣x2),由f′(x)=0得x=±![]() ,
,
由f′(x)<0得x>![]() 或x<﹣
或x<﹣![]() ,
,
由f′(x)>0得﹣![]() <x<
<x<![]() ,
,
∴f(x)的单调减区间为(﹣∞,﹣![]() ),(
),(![]() ,+∞).单调增区间为(﹣,
,+∞).单调增区间为(﹣,![]() ).
).
∴f(x)的极大值为f(![]() ),极小值为f(﹣
),极小值为f(﹣![]() ),故②正确.
),故②正确.
∵x<﹣![]() 时,f(x)<0恒成立.
时,f(x)<0恒成立.
∴f(x)无最小值,但有最大值f(![]() )
)
∴③不正确.
故选:D.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】为了防止受到核污染的产品影响民众的身体健康,某地要求这种产品在进入市场前必须进行两轮苛刻的核辐射检测,只有两轮检测都合格才能上市销售,否则不能销售。已知该产品第一轮检测不合格的概率为![]() ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为![]() ,每轮检测结果只有“合格”、“不合格”两种,且两轮检测是否合格相互之间没有影响。
,每轮检测结果只有“合格”、“不合格”两种,且两轮检测是否合格相互之间没有影响。
(1)求该产品不能上市销售的概率;
(2)如果这种产品可以上市销售,则每件产品可获利50元;如果这种产品不能上市销售,则每件产品亏损80元(即获利为![]() 80元)。现有这种产品4件,记这4件产品获利的金额为
80元)。现有这种产品4件,记这4件产品获利的金额为![]() 元,求
元,求![]() 的分布列。
的分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+3|x﹣a|(a∈R).
(1)若f(x)在[﹣1,1]上的最大值和最小值分别记为M(a),m(a),求M(a)﹣m(a);
(2)设b∈R,若[f(x)+b]2≤4对x∈[﹣1,1]恒成立,求3a+b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形ABCD的边长为2,∠BAD=120°,点E、F分别在边BC、DC上, ![]() =λ
=λ ![]() ,
, ![]() =μ
=μ ![]() ,若
,若 ![]()
![]() =1,
=1, ![]()
![]() =﹣
=﹣ ![]() ,则λ+μ=( )
,则λ+μ=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知q和n均为给定的大于1的自然数,设集合M={0,1,2,…,q﹣1},集合A={x|x=x1+x2q+…+xnqn﹣1 , xi∈M,i=1,2,…n}.
(1)当q=2,n=3时,用列举法表示集合A;
(2)设s,t∈A,s=a1+a2q+…+anqn﹣1 , t=b1+b2q+…+bnqn﹣1 , 其中ai , bi∈M,i=1,2,…,n.证明:若an<bn , 则s<t.
查看答案和解析>>
科目:高中数学 来源: 题型:
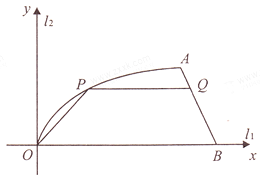
【题目】如图,某小区内有两条互相垂直的道路![]() 与
与![]() ,平面直角坐标系
,平面直角坐标系![]() 的第一象限有一块空地
的第一象限有一块空地![]() ,其边界
,其边界![]() 是函数
是函数![]() 的图象,前一段曲线
的图象,前一段曲线![]() 是函数
是函数![]() 图象的一部分,后一段
图象的一部分,后一段![]() 是一条线段.测得
是一条线段.测得![]() 到
到![]() 的距离为8米,到
的距离为8米,到![]() 的距离为16米,
的距离为16米,![]() 长为20米.
长为20米.
(1)求函数![]() 的解析式;
的解析式;
(2)现要在此地建一个社区活动中心,平面图为梯形![]() (其中
(其中![]() ,
,![]() 为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以A表示值域为R的函数组成的集合,B表示具有如下性质的函数φ(x)组成的集合:对于函数φ(x),存在一个正数M,使得函数φ(x)的值域包含于区间[﹣M,M].例如,当φ1(x)=x3 , φ2(x)=sinx时,φ1(x)∈A,φ2(x)∈B.现有如下命题:
①设函数f(x)的定义域为D,则“f(x)∈A”的充要条件是“b∈R,a∈D,f(a)=b”;
②函数f(x)∈B的充要条件是f(x)有最大值和最小值;
③若函数f(x),g(x)的定义域相同,且f(x)∈A,g(x)∈B,则f(x)+g(x)B.
④若函数f(x)=aln(x+2)+ ![]() (x>﹣2,a∈R)有最大值,则f(x)∈B.
(x>﹣2,a∈R)有最大值,则f(x)∈B.
其中的真命题有 . (写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】狄利克雷函数是高等数学中的一个典型函数,若![]() ,则称
,则称![]() 为狄利克雷函数.对于狄利克雷函数
为狄利克雷函数.对于狄利克雷函数![]() ,给出下面4个命题:①对任意
,给出下面4个命题:①对任意![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ;③对任意
;③对任意![]() ,都有
,都有![]() ,
, ![]() ;④对任意
;④对任意![]() ,都有
,都有![]() .其中所有真命题的序号是( )
.其中所有真命题的序号是( )
A. ①④ B. ②③ C. ①②③ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com