
 设函数f(x)=log2(x-a)(a∈R).
设函数f(x)=log2(x-a)(a∈R).分析 (1)当a=2,根据对数方程的性质解方程即可得到结论.
(2)根据对数函数的性质,结合对数函数的性质进行求解即可.
解答 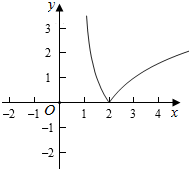 解:(1)当a=2时,f(x)=log2(x-2),
解:(1)当a=2时,f(x)=log2(x-2),
则方程f(x)-f(x+1)=-1等价为log2(x-2)-log2(x-1)=-1,
即1+log2(x-2)=log2(x-1),
即log22(x-2)=log2(x-1),
则2(x-2)=x-1,即x=3,此时log2(3-2)-log2(3-1)=0-1=-1,方程成立.
即方程的解集为{3}.
(2)当a=1时,f(x)=log2(x-1),
则y=|log2(x-1)|=$\left\{\begin{array}{l}{lo{g}_{2}(x-1),}&{x≥2}\\{-lo{g}_{2}(x-1),}&{1<x<2}\end{array}\right.$,
则对应的图形为,
则函数的定义域为(1,+∞),
函数的值域为[0,+∞),
函数为非奇非偶函数,
函数的单调递减区间为为(1,2),函数的单调递增区间为[2,+∞).
点评 本题主要考查对数方程和对数函数的图象和性质的考查,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | x1+x2=2 | B. | 9<x3•x4<25 | C. | 0<(6-x3)•(6-x4)<1 | D. | 1<x1•x2<9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
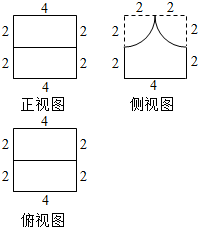 某几何体的三视图如图所示(其中侧视图为正方形上半部分在两个角上各截去四分之一圆),则该几何体的表面积为( )
某几何体的三视图如图所示(其中侧视图为正方形上半部分在两个角上各截去四分之一圆),则该几何体的表面积为( )| A. | 48+4π | B. | 48+8π | C. | 64+4π | D. | 64+8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f-1(x)=$\sqrt{x-1}$(3<x<8) | B. | f-1(x)=$\sqrt{x+1}$(3<x<8) | C. | f-1(x)=$\sqrt{x-1}$(4<x<9) | D. | f-1(x)=$\sqrt{x+1}$(4<x<9) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “b2=ac”是“a,b,c成等比数列”的充要条件 | |
| B. | “?x∈R,x2>0”的否定是“?x0∈R,x02>0” | |
| C. | “若a=-4,则函数f(x)=ax2+4x-1只有唯一一个零点”的逆命题为真命题 | |
| D. | “函数f(x)=lnx2与函数g(x)=$\left\{\begin{array}{l}{2lnx,x>0}\\{2ln(-x),x<0}\end{array}\right.$的图象相同” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com