
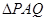 中,
中,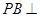 平面
平面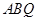 ,
,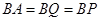 ,
,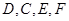 分别是
分别是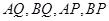 的中点,
的中点,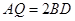 ,
,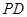 与
与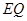 交于
交于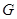 ,
,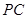 与
与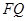 交于点
交于点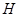 ,连接
,连接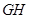 。
。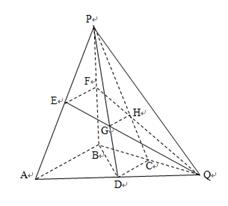
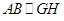 ;
; 的余弦值。
的余弦值。
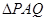 中,
中,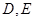 分别是
分别是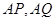 的中点,则
的中点,则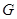 是
是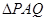 的重心,
的重心,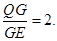
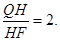 所以
所以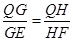 ,因此
,因此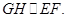
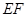 是
是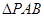 的中位线,所以
的中位线,所以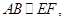
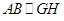 .
.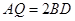 ,所以
,所以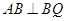 ,又
,又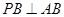 ,
,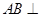 平面
平面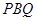 ,
,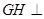 平面
平面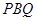 ,
,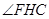 为二面角
为二面角 的平面角,
的平面角,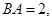 由三角形知识可得
由三角形知识可得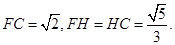
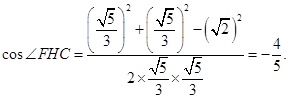
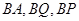 所在直线为
所在直线为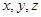 轴建立空间直角坐标系,不妨设
轴建立空间直角坐标系,不妨设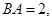 则
则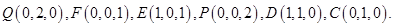
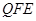 的法向量为
的法向量为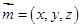 ,则
,则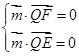 ,所以
,所以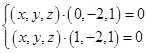 ,令
,令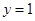 得
得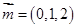
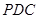 的一个法向量为
的一个法向量为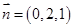 ,
,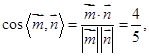
 的余弦值为
的余弦值为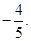
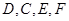 分别是
分别是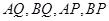 的中点,
的中点,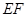 ∥
∥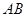 ,
,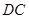 ∥
∥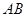 ,所以
,所以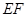 ∥
∥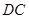 ,
,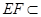 平面
平面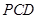 ,
,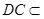 平面
平面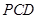 ,
,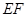 ∥平面
∥平面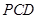 ,
,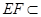 平面
平面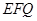 ,平面
,平面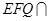 平面
平面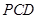
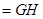 ,
,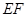 ∥
∥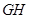 ,
,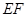 ∥
∥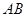 ,
,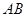 ∥
∥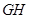 .
.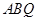 中,
中, 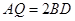 ,
,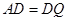 ,
,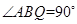 ,即
,即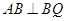 ,因为
,因为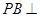 平面
平面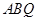 ,所以
,所以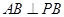 ,
,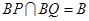 ,所以
,所以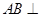 平面
平面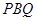 ,由(Ⅰ)知
,由(Ⅰ)知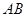 ∥
∥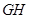 ,
,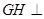 平面
平面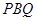 ,又
,又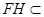 平面
平面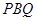 ,所以
,所以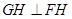 ,同理可得
,同理可得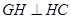 ,
,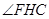 为二面角
为二面角 的平面角,设
的平面角,设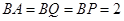 ,连接
,连接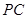 ,
,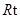 △
△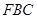 中,由勾股定理得,
中,由勾股定理得,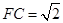 ,
,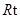 △
△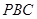 中,由勾股定理得,
中,由勾股定理得,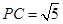 ,
,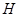 为△
为△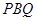 的重心,所以
的重心,所以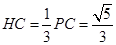
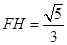 ,
,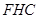 中,由余弦定理得
中,由余弦定理得 ,
, 的余弦值为
的余弦值为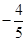 .
.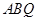 中,
中,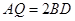 ,
,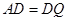 ,
,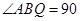 ,又
,又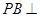 平面
平面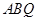 ,所以
,所以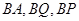 两两垂直,
两两垂直,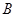 为坐标原点,分别以
为坐标原点,分别以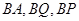 所在直线为
所在直线为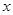 轴,
轴,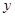 轴,
轴,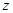 轴,建立如图所示的空间直角坐标系,设
轴,建立如图所示的空间直角坐标系,设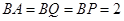 ,则
,则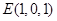 ,
,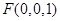 ,
,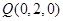 ,
,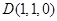 ,
,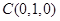
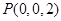 ,,所以
,,所以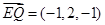 ,
,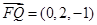 ,
,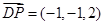 ,
,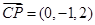 ,
,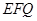 的一个法向量为
的一个法向量为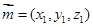 ,
,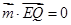 ,
,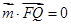 ,
,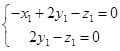
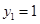 ,得
,得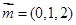 .
.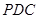 的一个法向量为
的一个法向量为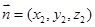
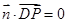 ,
,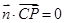 ,
,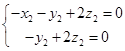
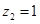 ,得
,得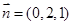 .所以
.所以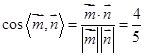
 为钝角,所以二面角
为钝角,所以二面角 的余弦值为
的余弦值为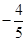 .
.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:不详 题型:解答题
 中,
中, ,
, ,
, 分别是
分别是 上的点,
上的点, ,
, 为
为 的中点.将
的中点.将 沿
沿 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥 ,其中
,其中 .
.
 平面
平面 ;
; 的平面角的余弦值.
的平面角的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
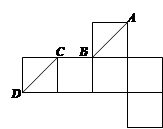
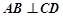 B.
B. 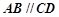
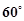 D. AB与CD相交
D. AB与CD相交查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
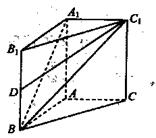
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
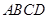 的对棱
的对棱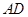 、
、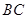 成
成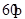 的角,且
的角,且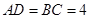 ,平行于
,平行于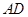 与
与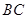 的截面分别交
的截面分别交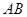 、
、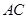 、
、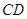 、
、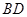 于
于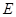 、
、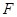 、
、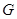 、
、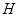 .
.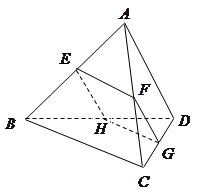
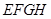 为平行四边形;
为平行四边形;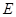 在
在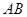 的何处时截面
的何处时截面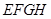 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com