
【题目】已知项数为![]() 的数列
的数列![]() 满足条件:①
满足条件:①![]() ;②
;②![]() ;若数列
;若数列![]() 满足
满足![]() ,则称
,则称![]() 为数列
为数列![]() 的“关联数列.
的“关联数列.
(1)数列1,5,9,13,17是否存在“关联数列”?若存在,写出其“关联数列”,若不存在,请说明理由;
(2)若数列![]() 存在“关联数列”
存在“关联数列”![]() ,证明:
,证明:![]() ;
;
(3)已知数列![]() 存在“关联数列”
存在“关联数列”![]() ,且
,且![]() ,
,![]() ,求数列
,求数列![]() 项数m的最小值与最大值.
项数m的最小值与最大值.
科目:高中数学 来源: 题型:
【题目】已知![]() ,其中
,其中![]() 是实常数.
是实常数.
(1)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() ,求证:函数
,求证:函数![]() 的零点有且仅有一个;
的零点有且仅有一个;
(3)若![]() ,设函数
,设函数![]() 的反函数为
的反函数为![]() ,若
,若![]() 是公差
是公差![]() 的等差数列且均在函数
的等差数列且均在函数![]() 的值域中,求证:
的值域中,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线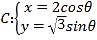 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程
的极坐标方程![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是国家统计局于2020年1月9日发布的2018年12月到2019年12月全国居民消费价格的涨跌幅情况折线图.(注:同比是指本期与同期作对比;环比是指本期与上期作对比.如:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比)根据该折线图,下列结论错误的是( )
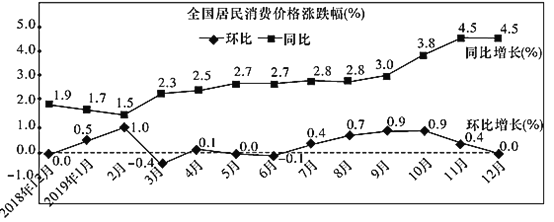
A.2019年12月份,全国居民消费价格环比持平
B.2018年12月至2019年12月全国居民消费价格环比均上涨
C.2018年12月至2019年12月全国居民消费价格同比均上涨
D.2018年11月的全国居民消费价格高于2017年12月的全国居民消费价格
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校开设了射击选修课,规定向![]() 、
、![]() 两个靶进行射击:先向
两个靶进行射击:先向![]() 靶射击一次,命中得1分,没有命中得0分,向
靶射击一次,命中得1分,没有命中得0分,向![]() 靶连续射击两次,每命中一次得2分,没命中得0分;小明同学经训练可知:向
靶连续射击两次,每命中一次得2分,没命中得0分;小明同学经训练可知:向![]() 靶射击,命中的概率为
靶射击,命中的概率为![]() ,向
,向![]() 靶射击,命中的概率为
靶射击,命中的概率为![]() ,假设小明同学每次射击的结果相互独立.现对小明同学进行以上三次射击的考核.
,假设小明同学每次射击的结果相互独立.现对小明同学进行以上三次射击的考核.
(1)求小明同学恰好命中一次的概率;
(2)求小明同学获得总分![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为5的菱形ABCD沿对角线AC折起,顶点B移动至![]() 处,在以点B',A,C,为顶点的四面体AB'CD中,棱AC、B'D的中点分别为E、F,若AC=6,且四面体AB'CD的外接球球心落在四面体内部,则线段EF长度的取值范围为( )
处,在以点B',A,C,为顶点的四面体AB'CD中,棱AC、B'D的中点分别为E、F,若AC=6,且四面体AB'CD的外接球球心落在四面体内部,则线段EF长度的取值范围为( )
A.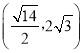 B.
B. C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com