定义在R+上的函数f(x)满足:
(1)存在a>1,使f(a)≠0;
(2)对任意的实数b,有f(xb)=bf(x).若方程f(mx)•f(mx2)=4f2(a)的所有解大于1,求m的取值范围.
解:令t=x
b,则b=log
xt,
则f(t)=log
xt•f(x)
即log
xt=
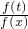
若f(mx)•f(mx
2)=4f
2(a)的所有解大于1,
则
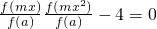
的所有解大于1,
即log
a(mx)•log
a(mx
2)-4=0的所有解大于1,
即2log
a2x+3log
am•log
ax+log
a2m-4=0的所有解大于1,
令u=log
ax,由a>1,
则u
2x+3log
am•u+log
a2m-4=0的所有解大于0
由韦达定理可得
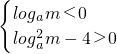
解得:0<m≤
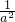
故m的取值范围为(0,
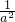
]
分析:令t=x
b,则b=log
xt,可得log
xt=
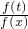
,进而根据方程f(mx)•f(mx
2)=4f
2(a)的所有解大于1,我们可以得到2log
a2x+3log
am•log
ax+log
a2m-4=0的所有解大于1,令u=log
ax,则u
2x+3log
am•u+log
a2m-4=0的所有解大于0,结合韦达定理,可以构造一个关于m的不等式组,解不等式组,即可得到答案.
点评:本题考查的知识点是函数与议程的综合应用,抽象函数的应用,其中根据已知条件,得到log
xt=
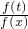
,从而将抽象问题具体化,是解答本题的关键.

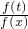
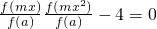 的所有解大于1,
的所有解大于1,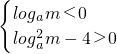
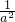
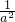 ]
]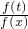 ,进而根据方程f(mx)•f(mx2)=4f2(a)的所有解大于1,我们可以得到2loga2x+3logam•logax+loga2m-4=0的所有解大于1,令u=logax,则u2x+3logam•u+loga2m-4=0的所有解大于0,结合韦达定理,可以构造一个关于m的不等式组,解不等式组,即可得到答案.
,进而根据方程f(mx)•f(mx2)=4f2(a)的所有解大于1,我们可以得到2loga2x+3logam•logax+loga2m-4=0的所有解大于1,令u=logax,则u2x+3logam•u+loga2m-4=0的所有解大于0,结合韦达定理,可以构造一个关于m的不等式组,解不等式组,即可得到答案.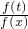 ,从而将抽象问题具体化,是解答本题的关键.
,从而将抽象问题具体化,是解答本题的关键. 
