数列
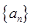
的前
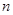
项和记为
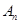
,
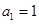
,
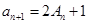
(
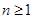
) (Ⅰ)求
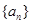
的通项公式;
(Ⅱ)等差数列
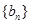
的各项为正,其前
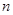
项和为
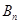
,且
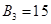
,又
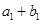
,
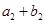
,
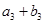
成等比数列,求
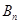
的表达式;
(3)若数列
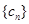
中
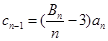
(
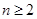
),求数列
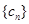
的前
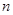
项和
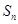
的
表达式.
(Ⅰ) 由
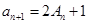
可得

(
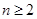
),
两式相减得

,于是
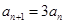
(
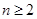
),
又

∴

,
故
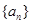
是首项为

,公比为

得等比数列, ∴

………………4分
(Ⅱ)设
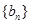
的公差为

, 由
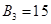
,可得

,得

,
故可设

,

又
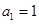
,

,

,
由题意可得

, 解得

,

,
∵等差数列

的各项为正,∴

,于是

,

; ……………………………8分
(3)

(
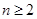
),

(
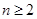
),

(
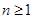
),

1
于是,

2
两式相减得:


.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
14分)已知在数列

中,

,

是其前

项和,且

.
(1)证明:数列
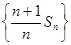
是等差数列;
(2)令

,记数列

的前

项和为

.
①;求证:当

时,

②: 求证:当

时,

查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设数列
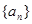
的前n项和为S
n=2n
2,
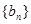
为等比数列,且
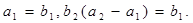
(Ⅰ)求数列
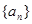
和
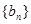
的通项公式;
(Ⅱ)设
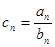
,求数列
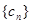
的前n项和T
n.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知数列

满足

,则数列

的通项

_______________.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设
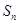
为等差数列

的前

项和,若

,公差

,

,则

________
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分10分)
设

给定数列

,

(1)求证:

(2)求证:数列

是单调递减数列.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知
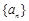
是公比为
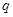
的等比数列,且
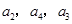
成等差数列,则
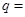
_______
查看答案和解析>>

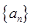 的前
的前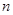 项和记为
项和记为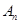 ,
,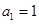 ,
,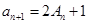 (
(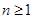 ) (Ⅰ)求
) (Ⅰ)求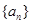 的通项公式;
的通项公式;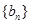 的各项为正,其前
的各项为正,其前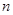 项和为
项和为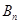 ,且
,且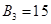 ,又
,又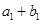 ,
,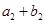 ,
,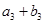 成等比数列,求
成等比数列,求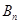 的表达式;
的表达式;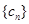 中
中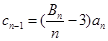 (
(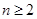 ),求数列
),求数列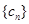 的前
的前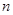 项和
项和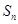 的
的 习题精选系列答案
习题精选系列答案