


 与z轴建立空间直角坐标系:
与z轴建立空间直角坐标系: 










 ,由法向量的定义得:
,由法向量的定义得:
 不妨设 z=1, 则
不妨设 z=1, 则 
 ,点P
,点P 平面EFG
平面EFG ∴AP∥平面EFG
∴AP∥平面EFG 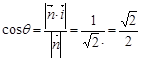 ,则它的一个法向量为
,则它的一个法向量为 =(1,0,0)
=(1,0,0) . 则
. 则  ,
,

 面PAB,∴AP∥平面EFG
面PAB,∴AP∥平面EFG 

 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源:不详 题型:解答题
 .
.
 ,EF =
,EF =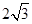 ,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?
,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com