
【题目】在△ABC中,a,b,c分别为角A,B,C所对的边.已知sinC= ![]() sinB,c=2,cosA=
sinB,c=2,cosA= ![]() .
.
(Ⅰ)求a的值;
(Ⅱ)求sin(2A﹣ ![]() )的值.
)的值.
【答案】解:(Ⅰ)∵△ABC中,a,b,c分别为角A,B,C所对的边.
sinC= ![]() sinB,∴由正弦定理可得c=
sinB,∴由正弦定理可得c= ![]() .
.
∵c=2,∴b=3,再根据cosA= ![]() =
= ![]() =
= ![]() ,∴a=
,∴a= ![]() .
.
(Ⅱ)∵cosA= ![]() ,∴sinA=
,∴sinA= ![]() =
= ![]() ,∴sin2A=2sinAcosA=
,∴sin2A=2sinAcosA= ![]() ,
,
cos2A=2cos2A﹣1= ![]() ,
,
∴sin(2A﹣ ![]() )=sin2Acos
)=sin2Acos ![]() ﹣cos2Asin
﹣cos2Asin ![]() =
= ![]()
![]() ﹣
﹣ ![]() =
= ![]()
【解析】(1)根据正弦定理和已知条件不难得到,c与b的大小关系,求出c的值,再根据余弦定理可得a的值,(2)由同角三角函数值的关系求得sinA,从而得到sin2A,cos2A,再由两角差的正弦公式可得结果.
【考点精析】通过灵活运用两角和与差的正弦公式,掌握两角和与差的正弦公式:![]() 即可以解答此题.
即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的部分图象如图所示,将y=f(x)的图象向右平移
)的部分图象如图所示,将y=f(x)的图象向右平移 ![]() 个单位长度后得到函数y=g(x)的图象.
个单位长度后得到函数y=g(x)的图象. 
(1)求函数y=g(x)的解析式;
(2)在△ABC中,角A,B,C满足2sin2 ![]() =g(C+
=g(C+ ![]() )+1,且其外接圆的半径R=2,求△ABC的面积的最大值.
)+1,且其外接圆的半径R=2,求△ABC的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A、B、C为锐角△ABC的三个内角,M=sinA+sinB+sinC,N=cosA+2cosB,则( )
A.M<N
B.M=N
C.M>N
D.M、N大小不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
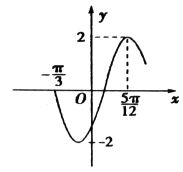
【题目】函数f(x)=Asin(ωx+φ),x∈R,(ω>0,﹣ ![]() <φ<
<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示.
(Ⅰ)确定A,ω,φ的值,并写出函数f(x)的解析式;
(Ⅱ)描述函数y=f(x)的图象可由函数y=sinx的图象经过怎样的变换而得到;
(Ⅲ)若f( ![]() )=
)= ![]() (
( ![]() <α<
<α< ![]() ),求tan2(α﹣
),求tan2(α﹣ ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数 ![]() .
.
(1)若f(x)是奇函数,求m的值;
(2)当m=1时,求函数f(x)在(﹣∞,0)上的值域,并判断函数f(x)在(﹣∞,0)上是否为有界函数,请说明理由;
(3)若函数f(x)在[0,1]上是以3为上界的函数,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率. 附:K2= ![]()
P(K2>k0) | 0.10 | 0.05 |
| 0.005 |
k0 | 2.706 | 3.841 |
| 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2BC,E,F,E1分别是棱AA1 , BB1 , A1B1的中点. 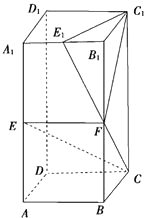
(1)求证:CE∥平面C1E1F;
(2)求证:平面C1E1F⊥平面CEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题“非空集合 ![]() 中的元素都是集合
中的元素都是集合 ![]() 中的元素”是假命题,
中的元素”是假命题,
那么下列命题中真命题的个数为( )
① ![]() 中的元素都不是
中的元素都不是 ![]() 中的元素 ②
中的元素 ② ![]() 中有不属于
中有不属于 ![]() 的元素
的元素
③ ![]() 中有属于
中有属于 ![]() 的元素 ④
的元素 ④ ![]() 中的元素不都是
中的元素不都是 ![]() 中的元素
中的元素
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com