练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在一个棱长为的正方体的表面涂上颜色，将其适当分割成棱长为的小正方体，全部放入不透明的口袋中，搅拌均匀后，从中任取一个，取出的小正方体表面仅有一个面涂有颜色的概率是（）

    A. B. C. D.

    【答案】C

    【解析】

    由在27个小正方体中选一个正方体，共有27种结果，满足条件的事件是取出的小正方体表面仅有一个面涂有颜色，有6种结果，根据古典概型及其概率的计算公式，即可求解．

    由题意，在27个小正方体中，恰好有三个面都涂色有颜色的共有8个，恰好有两个都涂有颜色的共12个，恰好有一个面都涂有颜色的共6个，表面没涂颜色的1个，

    可得试验发生包含的事件是从27个小正方体中选一个正方体，共有27种结果，满足条件的事件是取出的小正方体表面仅有一个面涂有颜色，有6种结果，所以所求概率为．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，圆的参数方程为（为参数），圆与圆外切于原点，且两圆圆心的距离，以坐标原点为极点，轴正半轴为极轴建立极坐标系．

    （1）求圆和圆的极坐标方程；

    （2）过点的直线、与圆异于点的交点分别为点和点，与圆异于点的交点分别为点和点，且.求四边形面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4—4：极坐标与参数方程

    在平面直角坐标系中，将曲线 (为参数) 上任意一点经过伸缩变换后得到曲线的图形．以坐标原点为极点，x轴的非负半轴为极轴，取相同的单位长度建立极坐标系，已知直线．

    （Ⅰ）求曲线和直线的普通方程；

    （Ⅱ）点P为曲线上的任意一点，求点P到直线的距离的最大值及取得最大值时点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （I）求函数的最大值；

    （II）当时，函数有最小值，记的最小值为，求函数的值域.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正项数列的前项和为，且和满足： ．

    （1）求的通项公式；

    （2）设，求的前项和；

    （3）在(2)的条件下，对任意,都成立，求整数的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂生产不同规格的一种产品，根据检测标准，其合格产品的质量与尺寸x（mm）之间近似满足关系式（b、c为大于0的常数）．按照某项指标测定，当产品质量与尺寸的比在区间内时为优等品．现随机抽取6件合格产品，测得数据如下：

    尺寸x（mm）

    38

    48

    58

    68

    78

    88

    质量y (g)

    16.8

    18.8

    20.7

    22.4

    24

    25.5

    质量与尺寸的比

    0.442

    0.392

    0.357

    0.329

    0.308

    0.290

    （Ⅰ）现从抽取的6件合格产品中再任选3件，记为取到优等品的件数，试求随机变量的分布列和期望；

    （Ⅱ）根据测得数据作了初步处理，得相关统计量的值如下表：

    75.3

    24.6

    18.3

    101.4

    （ⅰ）根据所给统计量，求y关于x的回归方程；

    （ⅱ）已知优等品的收益（单位：千元）与的关系为，则当优等品的尺寸x为何值时，收益的预报值最大？（精确到0.1）

    附：对于样本 ，其回归直线的斜率和截距的最小二乘估计公式分别为：，，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为了加强学生数学核心素养的培养，锻炼学生自主探究学习的能力，他们以教材第97页B组第3题的函数为基本素材，研究该函数的相关性质，取得部分研究成果如下：

    ①同学甲发现：函数是偶函数；

    ②同学乙发现：对于任意的都有；

    ③同学丙发现：对于任意的，都有；

    ④同学丁发现：对于函数定义域中任意的两个不同实数，总满足.

    其中所有正确研究成果的序号是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两支篮球队赛季总决赛采用7场4胜制，每场必须分出胜负，场与场之间互不影响，只要有一队获胜4场就结束比赛．现已比赛了4场，且甲篮球队胜3场．已知甲球队第5，6场获胜的概率均为，但由于体力原因，第7场获胜的概率为．

    （1）求甲队分别以，获胜的概率；

    （2）设表示决出冠军时比赛的场数，求的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知点是圆心为半径为的半圆弧上从点数起的第一个三等分点，点是圆心为半径为的半圆弧的中点，、分别是两个半圆的直径，，直线与两个半圆所在的平面均垂直，直线、共面.

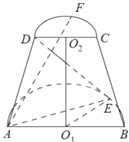
    （1）求三棱锥的体积；

    （2）求直线与所成角的余弦值.

    查看答案和解析>>

    同步练习册答案