练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （文科题）（本小题12分）

    （1）在等比数列{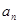 }中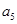，=162，公比q=3，前n项和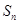=242，求首项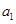和项数n的值．

    （2）已知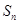是数列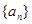的前n项和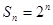，，求

     

    【答案】

    （1）；(2)  

    【解析】

    试题分析：(1)由=162，公比q=3,可求出a1,再根据等比数列前n项公式利用=242,得到关于n的方程求出n的值。

    (2)根据求通项即可。

    （1）由已知得 ………  3分

    解得………… 5分

    (2) …………7分

        

      ……… 10分

       ……………11分

           12分

    考点：等比数列的通项公式及前n项和公式，由Sn求an等知识。

    点评：.掌握等比数列的通项公式及前n项和公式是求解此类问题的关键，再由Sn求an时，要注意利用来求。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

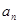
    科目：高中数学 来源： 题型：

    如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．
    （1）证明CD⊥AE；
    （2）证明PD⊥平面ABE；
    （3）求二面角A-PD-C的正切值．（本小题理科学生做，文科学生不做）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （文科做）已知点A1（2，0），A2（1，t），A3（0，b），A4（-1，t），A5（-2，0），其中t＞0，b为正常数．
    （1）半径为2的圆C1经过Ai（i=1，2，…，5）这五个点，求b和t的值；
    （2）椭圆C2以F1（-c，0），F2（c，0）（c＞0）为焦点，长轴长是4．若AiF1+AiF2=4（i=1，2，…，5），试用b表示t；
    （3）在（2）中的椭圆C2中，两线段长的差A1F1-A1F2，A2F1-A2F2，…，A5F1-A5F2构成一个数列{an}，求证：对n=1，2，3，4都有an+1＜an．（本小题解答中用到了椭圆的第一定义与焦半径公式，新教材实验区的学生可不解第三小题，请学习时注意）

    查看答案和解析>>

    科目：高中数学 来源：2013届广东省高二第二学期期中文科数学试卷（解析版） 题型：解答题

    (本小题满分12分)

        某中学采取分层抽样的方法从应届高三学生中按照性别抽取20名学生，

    其中8名女生中有3名报考理科，男生中有2名报考文科

       （1）是根据以上信息，写出列联表

       （2）用假设检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关？参考公式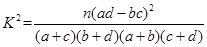

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

     

    2.07

    2.71

    3.84

    5.02

    6.64

    7.88

    10.83

     

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年广东省高三下学期期初考试数学理卷 题型：解答题

    （本小题满分13分）

    我校要用三辆汽车把高二文科学生从学校送到古田参加社会实践活动，已知学校到古田有两条公路，汽车走公路①堵车的概率为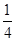，不堵车的概率为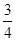；汽车走公路②堵车的概率为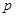，不堵车的概率为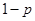．若甲、乙两辆汽车走公路①，丙汽车由于其他原因走公路②，且三辆车是否堵车相互之间没有影响

    （I）若三辆汽车中恰有一辆汽车被堵的概率为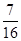，求汽车走公路②堵车的概率P。

    （II）在（1）的条件下，求三辆汽车中被堵车辆的个数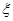的分布列和数学期望。

     

    查看答案和解析>>

    同步练习册答案