
分析 (1)由抛物线的定义知,点P的轨迹为抛物线,由此能求出动圆圆心的轨迹方程.
(2)设直线AB的方程为x=my+1,联立直线与抛物线,利用韦达定理、斜率公式,即可证明结论.
解答 解:由题意得:圆心P到点F的距离等于它到直线l的距离,
∴圆心P的轨迹是以F为焦点,直线l为准线的抛物线.
设圆心P的轨迹方程为y2=2px(p>0)(p>0).
∵$\frac{p}{2}$=1,
∴p=2.
∴圆心P的轨迹方程为:y2=4x;
证明:(2)设直线AB的方程为x=my+1,A(x1,y1),B(x2,y2)
联立直线与抛物线可得y2-4my-4=0,∴y1+y2=4m,y1y2=-4,
∴kMA+kMB=$\frac{{y}_{1}}{{x}_{1}+1}$+$\frac{{y}_{2}}{{x}_{2}+1}$=$\frac{(1+\frac{{y}_{1}{y}_{2}}{4})({y}_{1}+{y}_{2})}{({x}_{1}+1)({x}_{2}+1)}$=0,即直线MA,MB的斜率之和为定值.
点评 本题考查抛物线的定义与方程,考查直线与抛物线的位置关系,考查斜率的计算,属于中档题.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:选择题
| A. | A+C=2B | B. | B2=AC | C. | 3(B-A)=C | D. | A2+B2=A(B+C) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{28}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(x≠±3) | B. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(x≠±5) | ||
| C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1(x≠±3) | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1(x≠±5) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
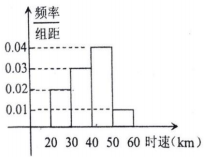 太原市某时段100辆汽车通过祥云桥时,时速的频率分布直方图如图所示,则时速在[30,40]的汽车约有( )
太原市某时段100辆汽车通过祥云桥时,时速的频率分布直方图如图所示,则时速在[30,40]的汽车约有( )| A. | 30辆 | B. | 35辆 | C. | 40辆 | D. | 50辆 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线 | B. | 圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com