
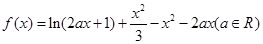
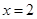 为
为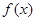 的极值点,求实数
的极值点,求实数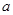 的值;
的值;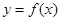 在
在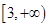 上为增函数,求实数
上为增函数,求实数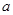 的取值范围;
的取值范围;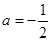 时,方程
时,方程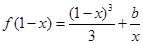 有实根,求实数
有实根,求实数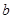 的最大值.
的最大值. ;(2)
;(2) ;(3)0.
;(3)0.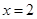 为
为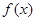 的极值点,所以
的极值点,所以 ,所以得出
,所以得出 ;(2)因为
;(2)因为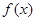 在区间
在区间 上为增函数,所以
上为增函数,所以 恒成立,通过对
恒成立,通过对 和
和 进行讨论;(3)将
进行讨论;(3)将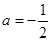 代入方程,得到
代入方程,得到 ,所以本题转化成
,所以本题转化成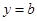 与
与 的交点问题,所以通过求导判断函数的单调性,画出函数
的交点问题,所以通过求导判断函数的单调性,画出函数 的图像,得到
的图像,得到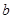 的取值范围.
的取值范围. 1分
1分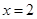 为
为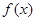 的极值点,所以
的极值点,所以 2分
2分 ,解得:
,解得: 3分
3分 时,
时, ,从而
,从而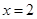 为
为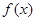 的极值点成立. 4分
的极值点成立. 4分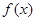 在区间
在区间 上为增函数,
上为增函数, 在区间
在区间 上恒成立. 5分
上恒成立. 5分 时,
时, 在
在 上恒成立,所以
上恒成立,所以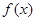 在
在 上为增函数,
上为增函数, 符合题意. 6分
符合题意. 6分 时,由函数
时,由函数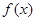 的定义域可知,必须有
的定义域可知,必须有 对
对 恒成立,故只能
恒成立,故只能 ,
, 在区间
在区间 上恒成立. 7分
上恒成立. 7分 ,其对称轴为
,其对称轴为 8分
8分 ,∴
,∴ ,从而
,从而 在
在 上恒成立,只要
上恒成立,只要 即可,
即可, ,解得:
,解得: 9分
9分 ,∴
,∴ .综上所述,
.综上所述,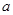 的取值范围为
的取值范围为 10分
10分 时,方程
时,方程 可化为,
可化为, .
. 在
在 上有解 11分
上有解 11分 ,则
,则 12分
12分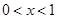 时,
时, ,∴
,∴ 在
在 上为增函数
上为增函数 时,
时, ,∴
,∴ 在
在 上为减函数
上为减函数 ,而
,而 ,故
,故 ,即实数
,即实数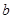 的最大值是0. 14分
的最大值是0. 14分

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源:不详 题型:解答题
 排,在路南侧沿直线
排,在路南侧沿直线 排,现要在矩形区域
排,现要在矩形区域 内沿直线将
内沿直线将 与
与 接通.已知
接通.已知 ,
, ,公路两侧排管费用为每米1万元,穿过公路的
,公路两侧排管费用为每米1万元,穿过公路的 部分的排管费用为每米2万元,设
部分的排管费用为每米2万元,设 与
与 所成的小于
所成的小于 的角为
的角为 .
.
 内的排管费用
内的排管费用 关于
关于 的函数关系式;
的函数关系式; .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 x2在(0,1 )上恒成立,求实数a的取值范围.
x2在(0,1 )上恒成立,求实数a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com