解:(1)空集是任何非空集合的真子集,故(1)不正确;
(2)根据奇函数的定义,对函数f(x)的定义域中的任一x的值,都有f(x)+f(-x)=0,条件f(1)+f(-1)=0并不能保证对定义域中任意x都有f(x)+f(-x)=0成立,故函数f(x)并不一定是奇函数,故(2)错误;
(3)函数
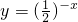
=2
x的反函数为y=log
2x;(3)正确;
(4)举反例如下:若f(x)=x在(-1,1)是增函数,但当x=0时,f(x)=0,函数y=2012f(x)-
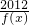
无意义,故(4)不正确;
(5)当x∈[0,+∞]时f(x)<1则0≤x<1 又∵偶函数关于y轴对称.∴f(x)<1的解集为{x|-1<x<1},则关于x不等式f(x-1)<1的解集为:-1<x-1<1,?x∈(0,2).故(5)正确.
故答案为:(3)(5).
分析:对于(1)空集是任何非空集合的真子集进行判定,对于(2)根据奇函数的定义进行判定,对于(3)根据反函数的求法进行判定,对于(4)举反例进行判定即可,对于(5)利用偶函数图象关于y轴对称,所以只需求出[0,+∞]内的范围,再根据对称性写出解集进行判断.
点评:本题考查命题的真假判断与应用,奇偶函数图象的对称性,反函数的等知识,注意应用举反例的方法否定结论,以便于判断真假.

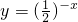 的反函数为y=log2x;
的反函数为y=log2x;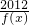 也是区间(a,b) 上的增函数;
也是区间(a,b) 上的增函数;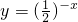 =2x的反函数为y=log2x;(3)正确;
=2x的反函数为y=log2x;(3)正确;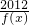 无意义,故(4)不正确;
无意义,故(4)不正确;
