
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用新定义“λ的相关函数”,对①②③④逐个判断即可得到答案.
解答 解:①、若f(x)为“1一半随函数”,则f(x+1)+f(x)=0,可得f(x+1)=-f(x),
可得f(x+2)=-f(x+1)=f(x),因此x=0,可得f(0)=f(2);故①正确;
②、假设f(x)=ax是一个“λ一半随函数”,则ax+λ+λax=0对任意实数x成立,
则有aλ+λ=0,而此式有解,所以f(x)=ax是“λ一半随函数”,故②正确.
③、令x=0,得f($\frac{1}{2}$)+$\frac{1}{2}$f(0)=0.所以f($\frac{1}{2}$)=-$\frac{1}{2}$f(0),
若f(0)=0,显然f(x)=0有实数根;若f(0)≠0,f($\frac{1}{2}$)•f(0)=-$\frac{1}{2}$(f(0))2<0,
又因为f(x)的函数图象是连续不断,所以f(x)在(0,$\frac{1}{2}$)上必有实数根,
因此任意的“-$\frac{1}{2}$一半随函数”必有根,即任意“-$\frac{1}{2}$一半随函数”至少有一个零点.故③正确.
④、假设f(x)=x2是一个“λ一半随函数”,则(x+λ)2+λx2=0,
即(1+λ)x2+2λx+λ2=0对任意实数x成立,所以λ+1=2λ=λ2=0,而此式无解,所以f(x)=x2不是一个“λ-同伴函数”.故④错误
正确判断:①②③.
故选:C.
点评 本题考查的知识点是函数的概念及构成要素,函数的零点,正确理解f(x)是λ-同伴函数的定义,是解答本题的关键.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-$\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 5-$\sqrt{2}$ | D. | $\sqrt{2}$-5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{3}<a<-\frac{3}{16}$ | B. | $-\frac{8}{5}<a<-\frac{3}{16}$ | C. | $-\frac{8}{3}<a<-\frac{1}{16}$ | D. | $-\frac{6}{5}<a<-\frac{3}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
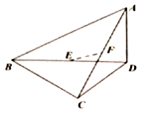 如图,三棱锥A-BCD中,BC⊥CD,AD⊥平面BCD,E、F分别为BD、AC的中点.
如图,三棱锥A-BCD中,BC⊥CD,AD⊥平面BCD,E、F分别为BD、AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com