
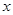 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为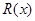 万元,且
万元,且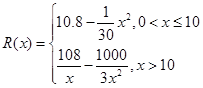 .
.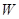 (万元)关于年产量
(万元)关于年产量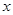 (千件)的函数关系式;
(千件)的函数关系式;
 千件时,该公司在这一品牌服装的生产中所获年利润最大,最大值为
千件时,该公司在这一品牌服装的生产中所获年利润最大,最大值为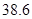 万元
万元 时,
时, ;
; 时,
时, .
.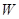 (万元)关于年产量
(万元)关于年产量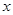 (千件)的函数关系式为
(千件)的函数关系式为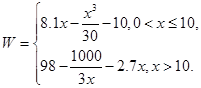 …………………6分
…………………6分 时,由
时,由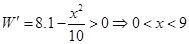 ,
,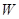 在
在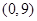 上单增,在
上单增,在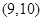 上单减
上单减 时,
时,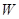 取得最大值,且
取得最大值,且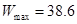 (万元).
(万元). 时,
时, ,仅当
,仅当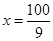 时取“=”
时取“=” 千件时,该公司在这一品牌服装的生产中所获年利润最大,最大值为
千件时,该公司在这一品牌服装的生产中所获年利润最大,最大值为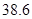 万元. …………………12分
万元. …………………12分

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:不详 题型:解答题
 的A,B两家工厂(视作污染源)的污染强度分别为
的A,B两家工厂(视作污染源)的污染强度分别为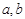 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数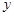 等于两家工厂对该处的污染指数之和.设
等于两家工厂对该处的污染指数之和.设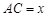 (
( ).
).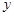 表示为
表示为 的函数;
的函数; ,且
,且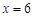 时,
时,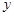 取得最小值,试求
取得最小值,试求 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
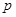 (万元)和
(万元)和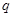 (万元),它们与投入的资金
(万元),它们与投入的资金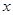 (万元)的关系,据经验估计为:
(万元)的关系,据经验估计为: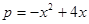 ,
,  今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?
今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
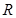 上的奇函数
上的奇函数 (
(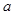 、
、 )过已知点
)过已知点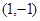 .
.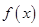 在区间
在区间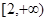 是增函数;若函数
是增函数;若函数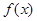 在区间
在区间 (其中
(其中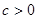 )也是增函数,求
)也是增函数,求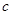 的最小值;
的最小值;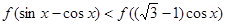 的解集.
的解集.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com