
分析 根据一元二次方程根的个数与△的关系,可求出k的范围,得到函数y=f(k)的定义域,利用韦达定理可得函数y=f(k)的解析式,结合二次函数的图象和性质,可得函数的图象和值域.
解答 解:∵x1,x2是关于x的方程x2-2(k-1)+k2-4=0的两个实数根,
∴△=4(k-1)2-4(k2-4)=-8k+16≥0,
解得:k≤2,
又∵x1+x2=2(k-1),x1•x2=k2-4,
∴y=x12+x22=(x1+x2)2-2x1•x2=2k2-8k+12,
故函数y=f(k)的解析式为y=2k2-8k+12,k≤2,
其图象如下图所示: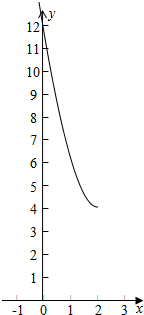
其定义域为(-∞,2],值域为[4,+∞)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
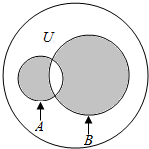 如图所示,最外层大圆围成区域表示全集U,大圈内层俩个小圆围成区域分别表示集合A,B,则图中阴影部分对应集合用已知集合结合相关集合运算表示为CU(A∩B)∩(A∪B).
如图所示,最外层大圆围成区域表示全集U,大圈内层俩个小圆围成区域分别表示集合A,B,则图中阴影部分对应集合用已知集合结合相关集合运算表示为CU(A∩B)∩(A∪B).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1],[1,2] | B. | [2,3],[3,4] | C. | [-2,-1],[1,2] | D. | [-2,-1],[3,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com