
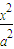 +
+ =1 (a>b>0).试问:当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为顶点,与C外切,与C1内接的平行四边形?并证明你的结论.
=1 (a>b>0).试问:当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为顶点,与C外切,与C1内接的平行四边形?并证明你的结论.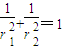 ,利用点在曲线上,即可求得结论.
,利用点在曲线上,即可求得结论.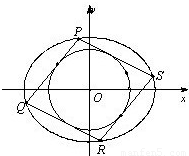
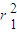 +
+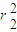 =
=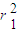
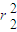 ,即
,即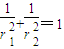
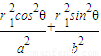 =1,即
=1,即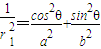
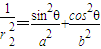 ,相加可得
,相加可得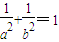
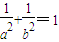 成立,则取P(r1cosθ,r1sinθ),Q(r2cos(θ+90°),r2sin(θ+90°)),
成立,则取P(r1cosθ,r1sinθ),Q(r2cos(θ+90°),r2sin(θ+90°)),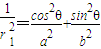 ,
,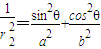 ,
,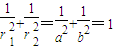


 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
| A、(-∞,-2)∪(2,+∞) | ||||||||
B、(-∞,-
| ||||||||
C、(-∞,-
| ||||||||
D、(-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com