已知函数
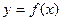
是
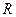
上的奇函数,当
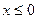
时,
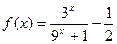
,
(1)判断并证明
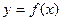
在
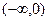
上的单调性;
(2)求
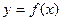
的值域;
(3)求不等式
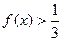
的解集。
解:(1)设

,则
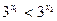
,

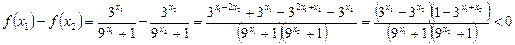
,
∴
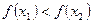
,即
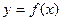
在
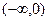
上是增函数。
(2)∵
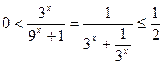
,∴当
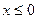
时,
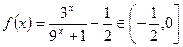
;
∵当
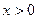
时,

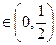
。
综上得
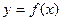
的值域为

。
(3)∵
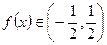
,又∵
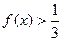
,∴
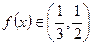
,
此时

单调递增,∵

,
∴
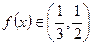
时,

。令

,
即

,
∴不等式
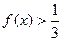
的解集是
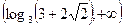
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
若函数
f(
x)=
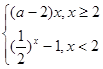
是R上的单调减函数,则实数
a的取值
范围是 ( )
| A.(-∞,2) | B.(-∞, ] ] | C.(0,2) | D.[ ,2) ,2) |
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(12分)已知2
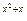
≤(
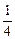
)
x-2,求函数y=2
x-2
-x的值域.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
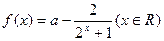
(1)若函数为奇函数

,求实数
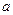
的值;
(2)在(1)的条件下,求函数
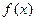
的值域
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
下列命题:①集合
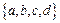
的子集个数有16个

;②定义在
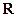
上的奇函数
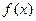
必满足

;③
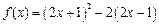
既不是奇函数又不是偶函数;④偶函数的图像一定与
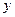
轴相

交;⑤
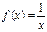
在
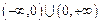
上是减函数。其中真命题的序号是
(把你认为正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设

上定义在R上的奇函数,且当

时,

,若
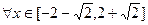
,不等式
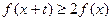
恒成立,则实数
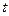
的取值范围是
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
当
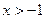
时,函数
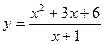
的最小值为__________________。
查看答案和解析>>

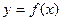 是
是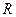 上的奇函数,当
上的奇函数,当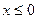 时,
时,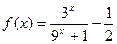 ,
,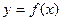 在
在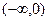 上的单调性;
上的单调性;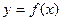 的值域;
的值域; 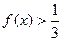 的解集。
的解集。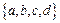 的子集个数有16个
的子集个数有16个 ;②定义在
;②定义在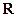 上的奇函数
上的奇函数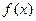 必满足
必满足 ;③
;③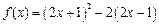 既不是奇函数又不是偶函数;④偶函数的图像一定与
既不是奇函数又不是偶函数;④偶函数的图像一定与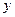 轴相
轴相 交;⑤
交;⑤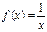 在
在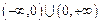 上是减函数。其中真命题的序号是 (把你认为正确的命题的序号都填上).
上是减函数。其中真命题的序号是 (把你认为正确的命题的序号都填上).