
【题目】在数列![]() 中.
中. ![]() ,
,![]()
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由,![]() 可得数列
可得数列![]() 是首项为4,公差为2的等差数列,从而可得
是首项为4,公差为2的等差数列,从而可得![]() 的通项公式;(2)由(1)可得
的通项公式;(2)由(1)可得![]()
![]() ,利用裂项相消法可得数列
,利用裂项相消法可得数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)![]() 的两边同时除以
的两边同时除以![]() ,得
,得![]() ,
,
所以数列![]() 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.
易得![]() ,所以
,所以![]() .
.
(2)由(1)知![]()
![]() ,
,
所以![]()
![]() .
.
【方法点晴】本题主要考查等差数列的定义与通项公式,以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:
(1)![]() ;(2)
;(2) ![]()
![]() ;
;
(3)![]() ;(4)
;(4)![]()
![]() ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.


科目:高中数学 来源: 题型:
【题目】用m,n表示两条不同的直线,α,β表示两个不同的平面,给出下列命题: ①若m⊥n,m⊥α,则n∥α;
②若m∥α,α⊥β则m⊥β;
③若m⊥β,α⊥β,则m∥α;
④若m⊥n,m⊥α,n⊥β,则α⊥β,
其中,正确命题是( )
A.①②
B.②③
C.③④
D.④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景点拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为36米,其中大圆弧所在圆的半径为14米,设小圆弧所在圆的半径为![]() 米,圆心角为
米,圆心角为![]() (弧度).
(弧度).
⑴ 求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
⑵ 已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为16元/米,设花坛的面积与装饰总费用之比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在封闭的直三棱柱ABC﹣A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,BC=8,AA1=5,则V的最大值是( )
A.4π
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2. 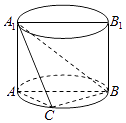
(1)求证:平面AA1C⊥平面BA1C;
(2)若AC=BC,求几何体A1﹣ABC的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,互相垂直的两条公路AP、AQ旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园AMN,要求点M在射线AP上,点N在射线AQ上,且直线MN过点C,其中AB=36米,AD=20米.记三角形花园AMN的面积为S. (Ⅰ)问:DN取何值时,S取得最小值,并求出最小值;
(Ⅱ)若S不超过1764平方米,求DN长的取值范围.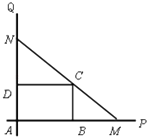
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A是△BCD所在平面外一点,M、N为△ABC和△ACD重心,BD=6; 
(1)求MN的长;
(2)若A、C的位置发生变化,MN的位置和长度会改变吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com