
【题目】如图所示,菱形![]() 与正方形
与正方形![]() 所在平面相交于
所在平面相交于![]() .
.

(1)求作平面![]() 与平面
与平面![]() 的交线
的交线![]() ,并说明理由;
,并说明理由;
(2)若![]() 与
与![]() 垂直且相等,求二面角
垂直且相等,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)过点![]() 作
作![]() 的平行线
的平行线![]() ,理由见解析;(2)
,理由见解析;(2)![]() .
.
【解析】
(1)过点![]() 作
作![]() 的平行线
的平行线![]() ,然后证明
,然后证明![]() 与
与![]() 平行,证明四边形
平行,证明四边形![]() 为平行四边形即可;
为平行四边形即可;
(2)取![]() 的中点
的中点![]() ,以其为坐标原点,建立空间直角坐标系,用向量坐标法求解即可.
,以其为坐标原点,建立空间直角坐标系,用向量坐标法求解即可.
解:(1)过点![]() 作
作![]() 的平行线
的平行线![]() 即可,下面予以证明.
即可,下面予以证明.
由已知易得,![]() 和
和![]() 都与
都与![]() 平行且相等,即
平行且相等,即![]() 与
与![]() 平行且相等.
平行且相等.
所以四边形![]() 是平行四边形,于是
是平行四边形,于是![]() .
.
又![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,![]() .
.
(2)由![]() ,
,![]() 且
且![]() ,得
,得![]() 平面
平面![]() .
.
由![]() 可得,
可得,![]() 是正三角形.
是正三角形.
取![]() 的中点
的中点![]() ,则
,则![]() .
.
建立如图所示的空间直角坐标系![]() .
.
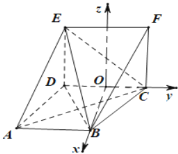
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量
的一个法向量![]()
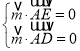 ,即
,即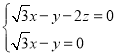 ,
,
令![]() ,则
,则![]() ,
,
得平面![]() 的一个法向量
的一个法向量![]()
设平面![]() 的一个法向量
的一个法向量![]()
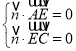 ,即
,即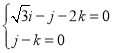 ,
,
令![]() ,则
,则![]() ,
,
得平面![]() 的一个法向量
的一个法向量![]() .
.
所以 .
.
故二面角![]() 余弦值为
余弦值为![]() .
.


科目:高中数学 来源: 题型:
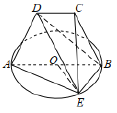
【题目】如图,![]() 是以
是以![]() 为直径的圆上一点,
为直径的圆上一点,![]() ,等腰梯形
,等腰梯形![]() 所在的平面垂直于⊙
所在的平面垂直于⊙![]() 所在的平面,且
所在的平面,且![]() .
.
(1)求![]() 与
与![]() 所成的角;
所成的角;
(2)若异面直线![]() 和
和![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)写出曲线C1和C2的直角坐标方程;
(2)已知P为曲线C2上的动点,过点P作曲线C1的切线,切点为A,求|PA|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知椭圆C:![]() (a>b>0)的短轴长为2,F1,F2分别是椭圆C的左、右焦点,过点F2的动直线与椭圆交于点P,Q,过点F2与PQ垂直的直线与椭圆C交于A、B两点.当直线AB过原点时,PF1=3PF2.
(a>b>0)的短轴长为2,F1,F2分别是椭圆C的左、右焦点,过点F2的动直线与椭圆交于点P,Q,过点F2与PQ垂直的直线与椭圆C交于A、B两点.当直线AB过原点时,PF1=3PF2.
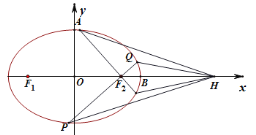
(1)求椭圆的标准方程;
(2)若点H(3,0),记直线PH,QH,AH,BH的斜率依次为![]() ,
,![]() ,
,![]() ,
,![]() .
.
①若![]() ,求直线PQ的斜率;
,求直线PQ的斜率;
②求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() ,直线
,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角的
的倾斜角的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图![]() ,
,![]() ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知
,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知![]() .
.
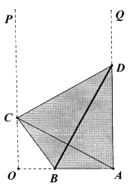
(1)若![]() ,求BD的长;
,求BD的长;
(2)问点C在何处时,规划区域的面积最小?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某便利店统计了今年第一季度各个品类的销售收入占比和净利润占比,并将部分品类的这两个数据制成如下统计图(注:销售收入占比![]() ,净利润占比
,净利润占比![]() ,净利润
,净利润![]() 销售收入
销售收入![]() 成本
成本![]() 各类费用),现给出下列判断:
各类费用),现给出下列判断:
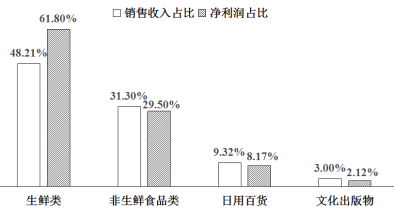
①该便利店第一季度至少有一种品类是亏损的;
②该便利店第一季度的销售收入中“生鲜类”贡献最大;
③该便利店第一季度“非生鲜食品类”的净利润一定高于“日用百货”的销售收入;
④该便利店第一季度“生鲜类”的销售收入比“非生鲜食品类”的销售收入多![]() .
.
则上述判断中正确的是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com