Question

若log₄（x+2y）+log₄（x-2y）=1，则|x|-|y|的最小值是    ．

Answer 1

【答案】分析：由函数的图象的对称性知，只考虑y≥0的情况即可，因为x＞0，所以只须求x-y的最小值．令x-y=u代入x²-4y²=4中，由判别式大于或等于零求出u的最小值，即为所求．
解答：解：由题意可得  ．
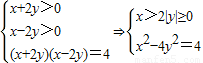
由函数的图象的对称性知，只考虑y≥0的情况即可，因为x＞0，所以只须求x-y的最小值．
令x-y=u代入x²-4y²=4中，有3y²-2uy+（4-u²）=0，
∵y∈R，∴△≥0，解得u≥．
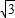
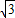
∴当时，u=，故|x|-|y|的最小值是．
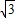
故答案为 ．
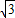
点评：本小题主要考查函数与函数的图象，函数图象的对称性的应用，求函数的最值，属于基础题．