
【题目】已知函数f(x)=lnx-a![]() .
.
(1)若a=-1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若f(x)![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】(1) x-y-2=0 (2) ![]()
【解析】
(1)利用曲线的切线方程公式,求得结果;
(2)由题,进行变形为f(x)![]() 恒成立,即f(x)
恒成立,即f(x)![]() 恒成立,构造新函数,用参变分离求函数单调性求其最值,求得a的范围.
恒成立,构造新函数,用参变分离求函数单调性求其最值,求得a的范围.
函数f(x)的定义域为(0,+![]() )
)
(1)a=-1时,f(x)=lnx-![]() .,
.,![]() ,
,
![]() ,且f(1)=-1.
,且f(1)=-1.
所以曲线![]() 在点(1,f(1))处的切线方程为y-(-1)=x-1,
在点(1,f(1))处的切线方程为y-(-1)=x-1,
即x-y-2=0.
(2)若f(x)![]() 恒成立,即f(x)
恒成立,即f(x)![]() 恒成立.
恒成立.
设g(x)=f(x)-x=lnx--a![]() ,只要
,只要![]() 即可;
即可;
![]() .
.
①当a=0时,令![]() ,得x=1.
,得x=1.
x,![]() 变化情况如下表:
变化情况如下表:
x | (0,1) | 1 | (1,+ |
| + | 0 | - |
g(x) | ↗ | 极大值 | ↘ |
所以![]() ,故满足题意.
,故满足题意.
②当a![]() 时,令
时,令![]() ,得x=-
,得x=-![]() (舍)或x=1;
(舍)或x=1;
x,![]() 变化情况如下表:
变化情况如下表:
x | (0,1) | 1 | (1,+ |
| + | 0 | - |
g(x) | ↗ | 极大值 | ↘ |
所以![]() ,令
,令![]() ,得
,得![]() .
.
③当![]() 时,存在x=2-
时,存在x=2-![]()
满足g(2-![]() )=ln(2-
)=ln(2-![]() )
)![]() ,
,
所以f(x)![]() 不能恒成立,所以
不能恒成立,所以![]() 不满足题意.
不满足题意.
综上,实数a的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() .
.
(2)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求
的体积最大时,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调节高三学生学习压力,某校高三年级举行了拔河比赛,在赛前三位老师对前三名进行了预测,于是有了以下对话:老师甲:“7班男生比较壮,7班肯定得第一名”.老师乙:“我觉得14班比15班强,14班名次会比15班靠前”.老师丙:“我觉得7班能赢15班”.最后老师丁去观看完了比赛,回来后说:“确实是这三个班得了前三名,且无并列,但是你们三人中只有一人预测准确”.那么,获得一、二、三名的班级依次为( )
A.7班、14班、15班B.14班、7班、15班
C.14班、15班、7班D.15班、14班、7班
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱柱ABC﹣A1B1C1中,平面AA1B1B⊥平面ABC,AB=AA1=A1B=4,BC=2,AC=2![]() ,点F为AB的中点,点E为线段A1C1上的动点.
,点F为AB的中点,点E为线段A1C1上的动点.
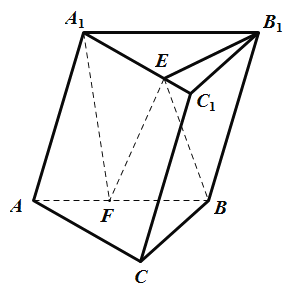
(1)求证:BC⊥平面A1EF;
(2)若∠B1EC1=60°,求四面体A1B1EF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 点左边)与直线
点左边)与直线![]() 交于点
交于点![]() .求
.求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,动直线l与椭圆E交于不同的两点
,动直线l与椭圆E交于不同的两点![]() ,
,![]() ,且△AOB的面积为1,其中O为坐标原点.
,且△AOB的面积为1,其中O为坐标原点.
(1)证明:![]() 为定值;
为定值;
(2)设线段AB的中点为M,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() 1(a
1(a![]() 0,b
0,b![]() 0)的左右焦点分别为F1,F2,点O为坐标原点,点P在双曲线的右支上,且满足|F1F2|=2|OP|.若直线PF2与双曲线C只有一个交点,则双曲线C的离心率为( )
0)的左右焦点分别为F1,F2,点O为坐标原点,点P在双曲线的右支上,且满足|F1F2|=2|OP|.若直线PF2与双曲线C只有一个交点,则双曲线C的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex﹣ax+a(a∈R),其图象与x轴交于A(x1,0),B(x2,0)两点,且x1<x2.
(1)求a的取值范围;
(2)证明:f′(![]() )<0(f′(x)为函数f(x)的导函数);
)<0(f′(x)为函数f(x)的导函数);
(3)设点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记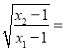 t,求(a﹣1)(t﹣1)的值.
t,求(a﹣1)(t﹣1)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为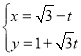 (t为参数),曲线C的极坐标方程为ρ=4sin(θ+
(t为参数),曲线C的极坐标方程为ρ=4sin(θ+![]() ).
).
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)若直线l与曲线C交于M,N两点,求△MON的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com