
| AP |
| AD |
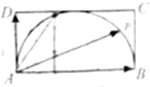
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
| π |
| 2 |
| 1 |
| 2 |
| 2sin2α+cos2α |
| 2 |
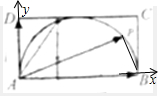 解:以A为坐标原点,AB,AD所在直线为x,y轴建立坐标系,
解:以A为坐标原点,AB,AD所在直线为x,y轴建立坐标系,| AB |
| AD |
| π |
| 2 |
| AP |
| AP |
| AB |
| AD |
| 1+cos2α |
| 2 |
| 1 |
| 2 |
| 2sin2α+cos2α |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 2 |
1+
| ||
| 2 |


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:
 已知直线l过点P(3,2).
已知直线l过点P(3,2).查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 2009 |
| 4 |
| 2011 |
| 2 |
| 2013 |
| 5 |
| A、c<a<b |
| B、a<c<b |
| C、c<b<a |
| D、a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 60岁以下 | 60岁以上 | 总计 | |
| 看生产日期与保质期 | 50 | 30 | 80 |
| 不看生产日期与保质期 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图是某居民小区年龄在20岁到45岁的居民上网情况的频率分布直方图,现已知年龄 在[30,35),[35,40),[40,45]的上网人数呈现递减的等差数列,则年龄在[35,40)的频( )
如图是某居民小区年龄在20岁到45岁的居民上网情况的频率分布直方图,现已知年龄 在[30,35),[35,40),[40,45]的上网人数呈现递减的等差数列,则年龄在[35,40)的频( )| A、0.04 | B、0.06 |
| C、0.2 | D、0.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com