Question

已知数列a₁,a₂,…,a₃₀,其中a₁,a₂,…,a₁₀是首项为1,公差为1的等差数列;a₁₀,a₁₁,…,a₂₀是公差为d的等差数列;a₂₀,a₂₁,…,a₃₀是公差为d²的等差数列(d≠0).

(1)若a₂₀=40,求d;

(2)试写出a₃₀关于d的关系式,并求a₃₀的取值范围;

(3)续写已知数列,使得a₃₀,a₃₁,…,a₄₀是公差为d³的等差数列,…,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题〔(2)应当作为特例〕,并进行研究,你能得到什么样的结论?

Answer 1

解：(1)a₁₀=10,a₂₀=10+10d=40,

    ∴d=3.

    (2)a₃₀=a₂₀+10d²=10(1+d+d²)(d≠0),

    a₃₀=10［(d+)²+］,

    当d∈(-∞,0)∪(0,+∞)时,a₃₀∈［7.5,10］∪(10,+∞).

    (3)所给数列可推广为无穷数列{a_n},其中a₁,a₂,…,a₁₀是首项为1,公差为1的等差数列,当n≥1时,数列a_10n,a_10n+1,…,a_10(n+1)是公差为dⁿ的等差数列.

 

    研究的问题可以是:试写出a_10(n+1)关于d的关系式,并求a_10(n+1)的取值范围.

    研究的结论可以是:由a₄₀=a₃₀+10d³=10(1+d+d²+d³),

    依次类推可得a_10(n+1)=10(1+d+…+dⁿ)=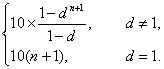

    当d＞0时,a_10(n+1)的取值范围为(10,+∞)等.