练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知双曲线C的方程为： ﹣ =1
    （1）求双曲线C的离心率；
    （2）求与双曲线C有公共的渐近线，且经过点A（﹣3，2 ）的双曲线的方程．

    【答案】
    （1）解：由题意知a2=9，b2=16，

    所以c2=a2+b2=25，

    则a=3，c=5，

    所以该双曲线的离心率e= =


    （2）解：根据题意，则可设双曲线的标准方程为 ﹣ =λ，（λ≠0）；

    又因为双曲线经过点A（﹣3，2 ）

    代入方程可得，λ= ；

    故这条双曲线的方程为 ﹣ =1


    【解析】（1）利用双曲线的方程的标准形式，求出a、b、c 的值，即得离心率的值．（2）根据题意中所给的双曲线的渐近线方，则可设双曲线的标准方程为 ，（λ≠0）；将点 代入方程，可得λ=﹣1；即可得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=cos2x+ sinxcosx．
    （Ⅰ）求函数f（x）的最小正周期及单调递增区间；
    （Ⅱ）求f（x）在区间[﹣ ， ]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数y=f（x）的定义域为{x|﹣2≤x≤3，且x≠2}，值域为{y|﹣1≤y≤2，且y≠0}，则y=f（x）的图象可能是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线y=﹣x+1与椭圆 + =1（a＞b＞0）相交于A、B两点，且线段AB的中点在直线l：x﹣2y=0上，求此椭圆的离心率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： + =1（a＞b＞0）的左右焦点分别为F1 ， F2 ， 抛物线y2=4x与椭圆C有相同的焦点，且椭圆C过点 ． （I）求椭圆C的标准方程；
    （Ⅱ）若椭圆C的右顶点为A，直线l交椭圆C于E、F两点（E、F与A点不重合），且满足AE⊥AF，若点P为EF中点，求直线AP斜率的最大值．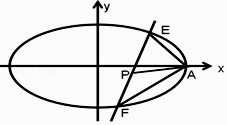

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某产品在某销售点的零售价x（单位：元）与每天的销售量y（单位：个）的统计数据如表所示：

    x

    16

    17

    18

    19

    y

    50

    34

    41

    31

    由表可得回归直线方程 中的 ，根据模型预测零售价为20元时，每天的销售量约为（ ）
    A.30
    B.29
    C.27.5
    D.26.5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，定圆C半径为2，A为圆C上的一个定点，B为圆C上的动点，若点A，B，C不共线，且| | |对任意t∈（0，+∞）恒成立，则 = ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在R上的函数f（x）满足f（0）=0，f（x）+f（1﹣x）=1，f（ ）= f（x）且当0≤x1＜x2≤1时，f（x1）≤f（x2），则f（ ）等于（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}满足a1=2，a2=4（a3﹣a4），数列{bn}满足bn=3﹣2log2an ．
    （1）求数列{an}，{bn}的通项公式；
    （2）令cn= ，求数列{cn}的前n项和Sn；
    （3）若λ＞0，求对所有的正整数n都有2λ2﹣kλ+2＞a2nbn成立的k的取值范围．

    查看答案和解析>>

    同步练习册答案